Python Program to find roots of a Quadratic Equation

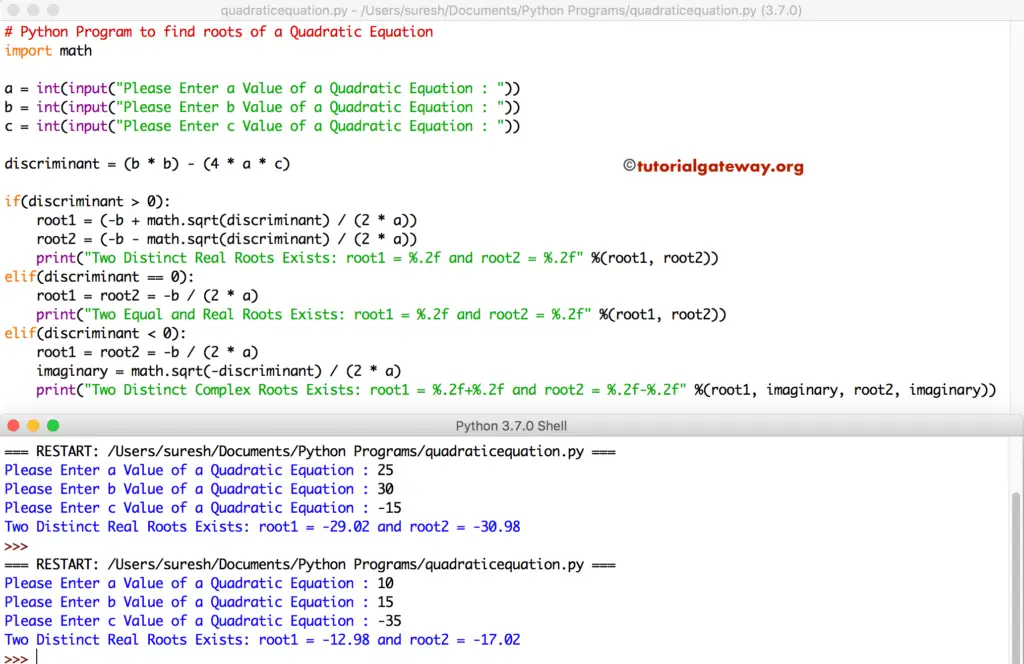
Write a Python program to find the Roots of a Quadratic Equation with an example. The mathematical representation of a Quadratic Equation is ax²+bx+c = 0. A Quadratic Equation can have two roots, and they depend entirely upon the discriminant. If discriminant > 0, then Two Distinct Real Roots exist for this equation

If discriminant = 0, Two Equal and Real Roots exist.

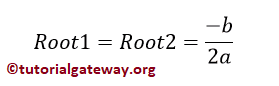
And if discriminant < 0, Two Distinct Complex Roots exist.

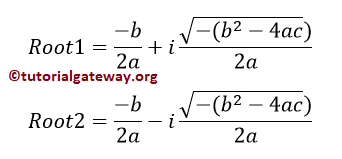
Python Program to find roots of a Quadratic Equation using elif

This Python program allows users to enter three values for a, b, and c. By using those values, this Python code finds the roots of a quadratic equation using Elif Statement. Please refer Python.

import math

a = int(input("Please Enter a Value of a Quadratic Equation : "))
b = int(input("Please Enter b Value of a Quadratic Equation : "))
c = int(input("Please Enter c Value of a Quadratic Equation : "))

discriminant = (b * b) - (4 * a * c)

if(discriminant > 0):
    root1 = (-b + math.sqrt(discriminant) / (2 * a))
    root2 = (-b - math.sqrt(discriminant) / (2 * a))
    print("Two Distinct Real Roots Exists: root1 = %.2f and root2 = %.2f" %(root1, root2))
elif(discriminant == 0):
    root1 = root2 = -b / (2 * a)
    print("Two Equal and Real Roots Exists: root1 = %.2f and root2 = %.2f" %(root1, root2))
elif(discriminant < 0):
    root1 = root2 = -b / (2 * a)
    imaginary = math.sqrt(-discriminant) / (2 * a)
    print("Two Distinct Complex Roots Exists: root1 = %.2f+%.2f and root2 = %.2f-%.2f" %(root1, imaginary, root2, imaginary))