The R Programming language introduced a new technique called Recursion or recursive functions for elegant and straightforward coding. Recursive means a function calling itself. In this article, we show how to write a simple program using R Recursive Functions with a practical example.
To understand the R recursive functions programming, let us consider a well-known yet simple example called factorial. We can calculate the factorial of any given number using the formula below.
n! = (n) * (n-1) * (n-2) * ….. * 1
It means, 6! = 6 * 5 * 4 * 3 * 2 * 1
We can achieve the same in R programming using For Loop, While Loop, etc. But if you observe the above pattern, its behavior is repetitive, which means recursive. So instead of writing the loops (costly), we can write the recursive functions R Programming.
# Example
Number.factorial <- function(number)
{
if(number == 0 || number == 1) {
return (1)
} else {
return (number * Number.factorial(number - 1))
}
}
Sum.Series(6)
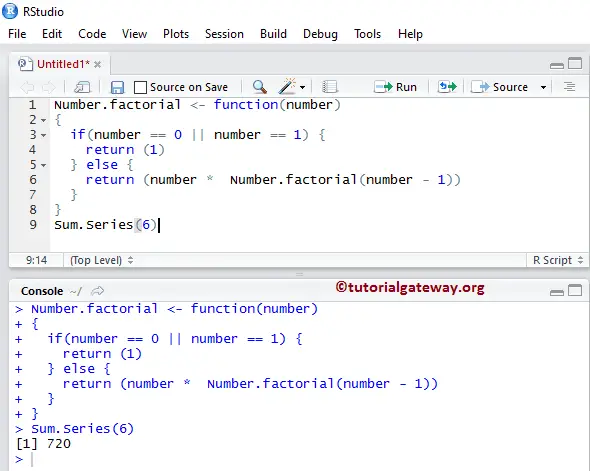
If we pass 0 or 1 as the Number argument value, then the R recursive function returns 1 else, it returns the below statement.
(number * Number.factorial(number - 1))
Let us calculate for 6!
6! = number * Number.factorial(number - 1) = 6 * Number.factorial (6 -1) = 6 * Number.factorial (5) # Recursively calling the above function = 6 * 5 * Number.factorial (5 -1) = 6 * 5 * Number.factorial (4) # Recursively calling the above function = 6 * 5 * 4 * Number.factorial (4 -1) = 6 * 5 * 4 * Number.factorial (3) # Recursively calling the above function = 6 * 5 * 4 * 3 * Number.factorial (3 -1) = 6 * 5 * 4 * 3 * Number.factorial (2) # Recursively calling the above function = 6 * 5 * 4 * 3 * 2 * Number.factorial (2 -1) = 6 * 5 * 4 * 3 * 2 * Number.factorial (1) # Recursively calling the above function = 6 * 5 * 4 * 3 * 2 * 1 = 720
Use Recursive Functions in R to Find Sum of Series 1²+2²+3²+…..+n²
In this example, we show how to write an R program to find the Sum of Series 1²+2²+3²+…..+n² using the Recursive Functions in R Programming. Please refer For Loop and While Loop articles.
# Example
Sum.Series <- function(number)
{
if(number == 0) {
return (0)
} else {
return ((number * number ) + Sum.Series(number - 1))
}
}
Sum.Series(5)
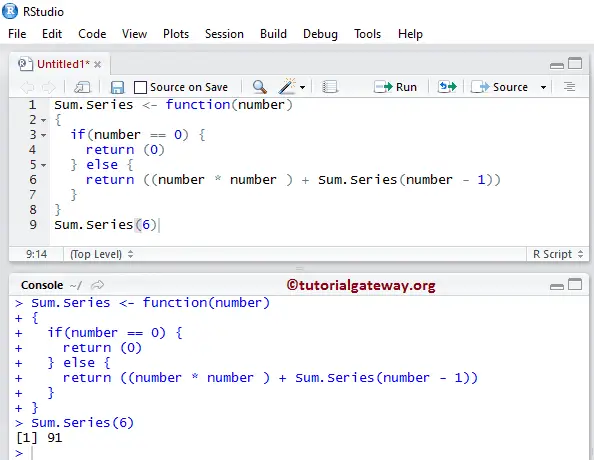
Let me show you the step by step execution process of the R recursive function.
Function Definition: Within the Sum.Series (number) function,
If the user entered Number is 0, then the function returns 0 else, it returns the following
(number * number ) + Sum.Series(number - 1)
Let us divide the above expression for a better understanding
- (number * number) = Multiplying the number
- Sum.Series(number – 1) = Calling the same function with decremented value (1 number minus)
From the above screenshot of Recursive Functions in R example, you can see the User entered value is 6:
Recursion 1: number = 6, which is Greater than 0
- (number * number ) + Sum.Series(number – 1)
- (6 * 6) + Sum.Series(6 – 1)
- 36 + Sum.Series(5)
2: number becomes 5, which is Greater than 0
- (number*number ) + Sum.Series(number – 1)
- (5 * 5) + Sum.Series(5 – 1)
- 25 + Sum.Series(4)
Total will be 36 + 25 = 61
Iteration 3: number becomes 4, which is Greater than 0
- (4 * 4) + Sum.Series(4 – 1)
- 16 + Sum.Series(3)
Total is 36 + 25 + 16 = 77
Recursion 4: number becomes 3, which is Greater than 0 so,
- (3 * 3) + Sum.Series(3 – 1)
- 9 + Sum.Series(2)
Total = 36 + 25 + 16 + 9 = 86
Recursion 5 : the number becomes 2, which is Greater than 0, so
- (2 * 2) + Sum.Series(2 – 1)
- 4 + Sum.Series(1)
Total will be 36 + 25 + 16 + 9 + 4 = 90
Recursion 6: the number becomes 1, which is Greater than 0.
- (1 * 1) + Sum.Series(1 – 1)
- 1 + Sum.Series(0)
Total = 36 + 25 + 16 + 9 + 4 + 1 = 91
Recursion 7: number becomes 0, which means First if condition is True, it exits from the function.
The final output is 91
We must use some conditions to exit from the recursive function calling in R. If you forgot the condition, then the function executes countless times (similar to Infinity Loop).
