Python Program to find Sum of Geometric Progression Series

Write a Python Program to find the Sum of the Geometric Progression Series (G.P. Series) with a practical example.

Python G.P. Series

A geometric Series is a sequence of elements in which the next item is obtained by multiplying a common ratio by the previous item. Or G.P. Series is a series of numbers in which a common ratio of any consecutive numbers (items) is always the same.

The mathematical formula behind this Sum of G.P Series
Sn = a(rⁿ) / (1- r)
Tn = ar^(n-1)

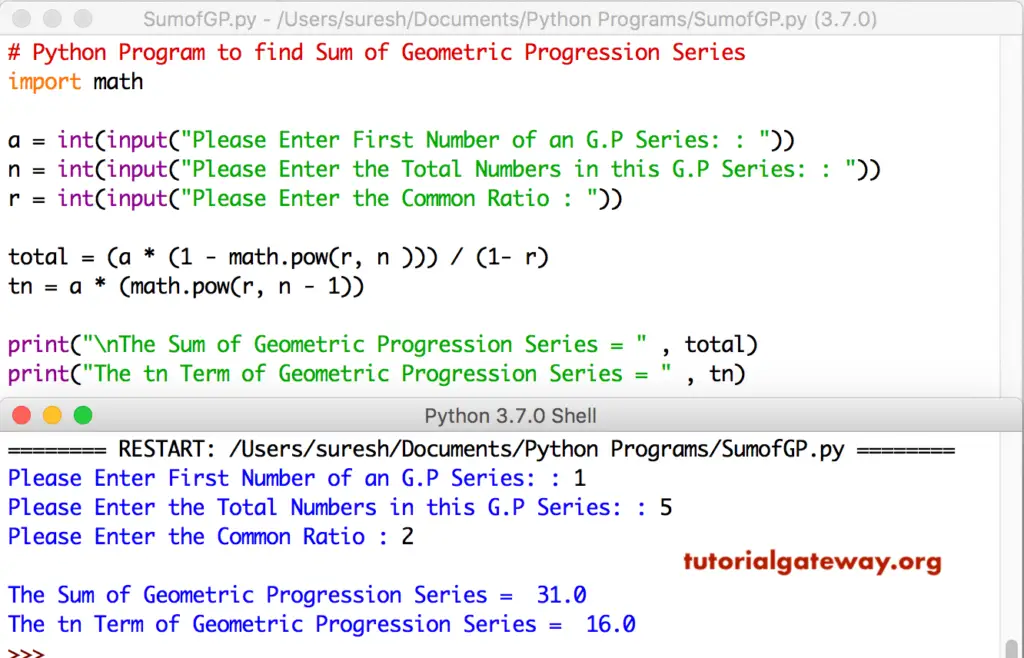
Python Program to Find Sum of Geometric Progression Series Example

This Python program allows the user to enter the first value, the total number of items in a series, and the common ratio. Next, it finds the sum of the Geometric Progression Series.

# Python Program to find Sum of Geometric Progression Series
import math

a = int(input("Please Enter First Number of an G.P Series: : "))
n = int(input("Please Enter the Total Numbers in this G.P Series: : "))
r = int(input("Please Enter the Common Ratio : "))

total = (a * (1 - math.pow(r, n ))) / (1- r)
tn = a * (math.pow(r, n - 1))

print("\nThe Sum of Geometric Progression Series = " , total)
print("The tn Term of Geometric Progression Series = " , tn)

Program to find the Sum of Geometric Progression Series without Math Formula

In this Python Program, we are not using any Mathematical formula.

# Python Program to find Sum of Geometric Progression Series

a = int(input("Please Enter First Number of an G.P Series: : "))
n = int(input("Please Enter the Total Numbers in this G.P Series: : "))
r = int(input("Please Enter the Common Ratio : "))

total = 0
value = a
print("\nG.P  Series :", end = " ")
for i in range(n):
    print("%d  " %value, end = " ")
    total = total + value
    value = value * r
    
print("\nThe Sum of Geometric Progression Series = " , total)

Python Sum of Geometric Progression Series output

Please Enter First Number of an G.P Series: : 1
Please Enter the Total Numbers in this G.P Series: : 5
Please Enter the Common Ratio : 4

G.P  Series : 1   4   16   64   256   
The Sum of Geometric Progression Series =  341

Python Program to Calculate Sum of Geometric Progression Series Using Functions

This Python Geometric Progression program is the same as the first example. However, in this Python program, we separated the logic using Functions.

# Python Program to find Sum of Geometric Progression Series
import math

def sumofGP(a, n, r):
    total = (a * (1 - math.pow(r, n ))) / (1- r)
    return total

a = int(input("Please Enter First Number of an G.P Series: : "))
n = int(input("Please Enter the Total Numbers in this G.P Series: : "))
r = int(input("Please Enter the Common Ratio : "))

total = sumofGP(a, n, r)
print("\nThe Sum of Geometric Progression Series = " , total)

Python Sum of G P Series output

Please Enter First Number of an G.P Series: : 2
Please Enter the Total Numbers in this G.P Series: : 6
Please Enter the Common Ratio : 3

The Sum of Geometric Progression Series =  728.0