Python Program to find Area of an Equilateral Triangle

Write a Python Program to find Area of an Equilateral Triangle, Perimeter, Semi Perimeter and Altitude of an Equilateral Triangle with example. Before we step into practical Python Program to find Area of an Equilateral Triangle example, Let see the definitions and formulas.

Area of an Equilateral Triangle Formula

The Equilateral Triangle is a triangle with all sides are equal and all of the angles are equal to 60 degrees. If we know the side of an Equilateral Triangle then, we can calculate the area of an Equilateral Triangle using below formula.

Area = (√3)/4 * s² (S = Any side of the Equilateral Triangle)

Perimeter is the distance around the edges. We can calculate perimeter using below formula:

Perimeter = 3s

We can calculate Semi Perimeter of an Equilateral Triangle using the formula: 3s/2 or we can simply say Perimeter/2.

We can calculate Altitude of an Equilateral Triangle using the formula: (√3)/2 * s

Python Program to find Area of an Equilateral Triangle

This python program allows the user to enter length of any one side of an Equilateral Triangle. Using this value we will calculate the Area, Perimeter, Semi Perimeter and Altitude of an Equilateral Triangle.

# Python Program to find Area of an Equilateral Triangle
import math

side = float(input('Please Enter Length of any side of an Equilateral Triangle: '))

# calculate the area
Area = (math.sqrt(3)/ 4)*(side * side)

# calculate the Perimeter
Perimeter = 3 * side

# calculate the semi-perimeter
Semi = Perimeter / 2

# calculate the Altitude
Altitude = (math.sqrt(3)/2)* side

print("\n Area of Equilateral Triangle = %.2f" %Area)
print(" Perimeter of Equilateral Triangle = %.2f" %Perimeter)
print(" Semi Perimeter of Equilateral Triangle = %.2f" %Semi)
print(" Altitude of Equilateral Triangle = %.2f" %Altitude)

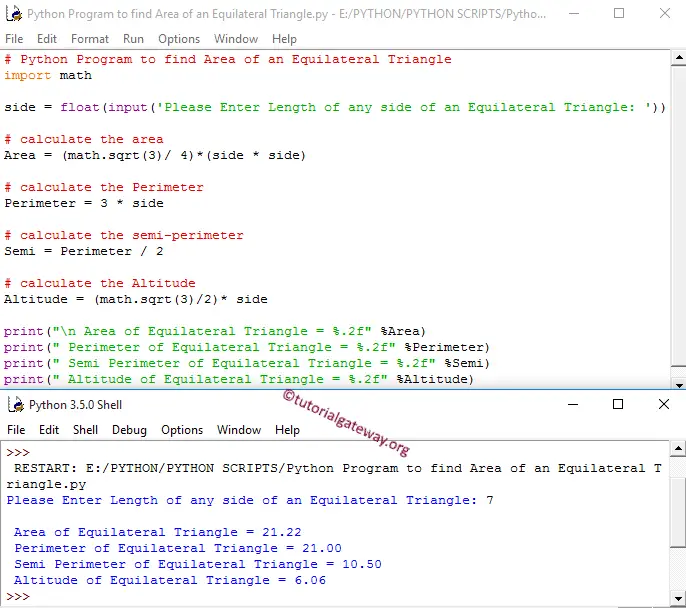
Within this Python Program to find Area of an Equilateral Triangle, the following statement will allow the User to enter the length of any side in the Equilateral Triangle.

side = float(input('Please Enter Length of any side of an Equilateral Triangle: '))

Next, we are calculating the Area of an Equilateral Triangle using the Formula:

Area = (math.sqrt(3)/ 4)*(side * side)

math.sqrt is the mathematical function, which is used to calculate the square root. Python will return error if we miss to use the import math

In the next line, We are calculating the Perimeter of an Equilateral Triangle using the formula

Perimeter = 3 * side

In the next line, We are calculating the semi perimeter of an Equilateral Triangle using the following formula. We can also find semi perimeter using the standard formula = (3 * side) / 2.

Semi = Perimeter / 2

In the next line, We are calculating the Altitude of an Equilateral Triangle using the formula:

Altitude = (math.sqrt(3)/2)* side

Following print statements will help us to print the Perimeter, Semi Perimeter, Altitude and Area of an Equilateral Triangle

print("\n Area of Equilateral Triangle = %.2f" %Area)
print(" Perimeter of Equilateral Triangle = %.2f" %Perimeter)
print(" Semi Perimeter of Equilateral Triangle = %.2f" %Semi)
print(" Altitude of Equilateral Triangle = %.2f" %Altitude)

Python Program to find Area of an Equilateral Triangle using functions

This python program allows the user to enter length of any one side of an Equilateral Triangle. We will pass that value to the function arguments to calculate the area of an equilateral triangle.

# Python Program to find Area of an Equilateral Triangle using Functions
import math

def Area_of_an_Equilateral_Triangle(side):
    # calculate the area
    Area = (math.sqrt(3)/ 4)*(side * side)
    
    # calculate the Perimeter
    Perimeter = 3 * side

    # calculate the semi-perimeter
    Semi = Perimeter / 2

    # calculate the Altitude
    Altitude = (math.sqrt(3)/2)* side

    print("\n Area of Equilateral Triangle = %.2f" %Area)
    print(" Perimeter of Equilateral Triangle = %.2f" %Perimeter)
    print(" Semi Perimeter of Equilateral Triangle = %.2f" %Semi)
    print(" Altitude of Equilateral Triangle = %.2f" %Altitude)

First, We defined the function with one argument using def keyword. It means, User will enter any one side of an equilateral triangle. Next, We are Calculating the an equilateral triangle as we described in our first example. The output of Python equilateral Triangle area is

>>> Area_of_an_Equilateral_Triangle(6)

 Area of Equilateral Triangle = 15.59
 Perimeter of Equilateral Triangle = 18.00
 Semi Perimeter of Equilateral Triangle = 9.00
 Altitude of Equilateral Triangle = 5.20
>>> Area_of_an_Equilateral_Triangle(12)

 Area of Equilateral Triangle = 62.35
 Perimeter of Equilateral Triangle = 36.00
 Semi Perimeter of Equilateral Triangle = 18.00
 Altitude of Equilateral Triangle = 10.39
>>>