The NumPy library is the shorter version for Numerical Python and the ndarray or array concept. This module is the foundation for introducing Data Science. The NumPy package has built-in functions that are required to perform Data Analysis and Scientific Computing.
All the other packages we use for data analysis are built on this module. That’s why one has to master this Python numpy ndarray array module before starting to work with DataFrames or Data analysis.
Creating Python Python numpy ndarray
The Numpy module has a ndarray object, a shorter version of N-dimensional, or an array. Like any other programming language, this Python Numpy ndarray object allows you to store multiple array items of the same data type.
The following is the list of available functions to create an Array by the Python numpy ndarray module.
- array function: which helps you to create an array object or convert the data from List, Tuple, or any sequence of items (something like range) to ndarray.
- asarray method: Use this to convert the input data to Python numpy ndarray array. However, it won’t copy if the given input is already a ndarray.
- zeros: Creates an array of 0’s of specified shape and type.
- zeros_like: Same as zeros. However, it takes another one to get shape and dtype.
- ones: Creates an array of 1’s of a given shape and datatype.
- ones_like: It accepts another to read its shape and datatype.
- empty, empty_like: These methods create an empty one by allocating some memory to them.
- arange: This creates or returns an array of elements in a given range. Same as the range method.
- eye, identity: creates a square identity matrix.
Create Python numpy ndarray Array using function
As we said earlier, the Numpy array method converts the given list, tuple, or any sequence for that matter. It is a simple example to create one.
import numpy as np arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) print(arr)
[1 2 3 4 5 6 7 8 9]Create Python numpy ndarray Array from List
Here, we declared an integer list of numbers from 1 to 5. Next, we used the Python numpy array function available in the module to convert that list.
We also created a new one of mixed items.
a = [1, 2, 3, 4, 5] arr = np.array(a) print(arr) b = [2.5, 3.5, 7, 4.5, 8] arr2 = np.array(b) print(arr2)
[1 2 3 4 5]
[2.5 3.5 7. 4.5 8. ]Let me create a ndarray from a list of lists. Here, we declared a nested list of lists with integer values. Next, we used this method to convert the list to arrays.
a = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print('List of List = ', a)
print()
arr = np.array(a)
print(arr)
Matrix from a list of lists output or a nested list.
List of List = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
[[1 2 3]
[4 5 6]
[7 8 9]]You might wonder, why don’t we use Lists when it looks the same?. These are meant to perform vectorized operations. When you perform any operation or use any method, that one is applied to each item.
We show those operations in the upcoming topic. However, we use a simple example to show you the same.
a = [1, 2, 3, 4, 5]
arr = np.array(a)
print('Original = ', arr)
print('Add 5 = ', arr + 5)
print('Multiply arr with 2 = ', arr * 2)
Vector operations on ndarray output.
Original = [1 2 3 4 5]
Add 5 = [ 6 7 8 9 10]
Multiply arr with 2 = [ 2 4 6 8 10]Create Python numpy ndarray Array from Tuple
You can also create a one-dimensional object from a Tuple.
tup = (10, 20, 30) arr = np.array(tup) print(arr)
Tuple to one-dimensional output
[10 20 30]Python numpy ndarray Two Dimensional array
Placing or Nesting two lists inside a [] brackets creates a two-dimensional Matrix.
two_arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]]) print(two_arr)
2D output
[[ 1 2 3 4 5]
[ 6 7 8 9 10]]Python numpy ndarray Three Dimensional Arrays
Here, we are creating a 3 * 3 matrix or multidimensional or three-dimensional.
three_arr = np.array([[1, 2, 3], [10, 20, 30], [6, 7, 8]]) print(three_arr)
Three-dimensional array output.
[[ 1 2 3]
[10 20 30]
[ 6 7 8]]Create a Numpy Array using srange
In this example, we are using the arange function to create an array of numbers ranging from 0 to n-1, where n is the given number. For example, np.arange(5) returns numbers in sequence from 0 to 4.
np.arange(5) np.arange(10) np.arange(15)
The srange method to create output. Add print
[0, 1, 2, 3, 4]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]Python numpy ndarray array using linspace
In this example, we used the linspace method to create it. The syntax behind this is:
np.linspace(start, end_value, steps)
Here, we created three arrays of numbers ranging from 0 to n serrated by steps. For example, np.linspace(0, 1, 5) returns the numbers from 0 to 1 in five equal steps.
print(np.linspace(0, 1, 5)) print(np.linspace(0, 10, 5)) print(np.linspace(0, 1, 7)) print(np.linspace(10, 100, 20))
linespace method output
[0. 0.25 0.5 0.75 1. ]
[ 0. 2.5 5. 7.5 10. ]
[0. 0.16666667 0.33333333 0.5 0.66666667 0.83333333
1. ]
[ 10. 14.73684211 19.47368421 24.21052632 28.94736842
33.68421053 38.42105263 43.15789474 47.89473684 52.63157895
57.36842105 62.10526316 66.84210526 71.57894737 76.31578947
81.05263158 85.78947368 90.52631579 95.26315789 100. ]
Apart from the method, the NumPy module has a few other ones to create it. They are 0’s, ones, and empty methods.
Python numpy ndarray zeros arrays
The zeros method creates an array of 0’s. It accepts the arguments to specify the shape. For example,
- zeros(2) means a one-dimensional of two 0 elements.
- zeros(2, 3) means 2 * 3 matrix of 0s.
- and (2, 2, 7) means a three-dimensional of 0’s.
print(np.zeros(3)) print(np.zeros((2, 2))) print(np.zeros((2, 3))) print(np.zeros((4, 7))) print(np.zeros((3, 2, 7)))
[0. 0. 0.]
[[0. 0.]
[0. 0.]]
[[0. 0. 0.]
[0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]]
[[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0.]]]Python numpy ndarray ones array
The ones function to create an array of 1’s. This ones method accepts the arguments to specify the number of items of it. For example,
- ones(4) means a one-dimensional of four 1’s.
- ones(2, 4) means 2 * 4 matrix of ones and ones(2, 3, 4) means 3D = 2 * 3 * 4 of 1’s.
print(np.ones(5)) print(np.ones((3, 3))) print(np.ones((3, 5))) print(np.ones((3, 2, 9)))
[1. 1. 1. 1. 1.]
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
[[[1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]]
[[1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]]
[[1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1.]]]Python Numpy random array
Use the random function to create an array of random numbers. Please visit Random article
print(np.random.random(5)) print(np.random.random((4, 4))) print(np.random.random((2, 3, 4)))
[0.17481245, 0.20246847, 0.95714739, 0.93449316, 0.00816149]
[[0.19520415, 0.73605745, 0.27957035, 0.39129715],
[0.3622134 , 0.10631005, 0.29756787, 0.49672655],
[0.32448671, 0.53070647, 0.09666927, 0.9382703 ],
[0.77069343, 0.75228313, 0.65435786, 0.13130023]]
[[[0.13560378, 0.41655648, 0.60812992, 0.87341762],
[0.82085101, 0.02908754, 0.1446217 , 0.1984121 ],
[0.97777709, 0.95961773, 0.75990116, 0.87158335]],
[[0.88883459, 0.55730694, 0.45067219, 0.89653719],
[0.39533872, 0.63479585, 0.23116183, 0.56565847],
[0.25483409, 0.7929711 , 0.80572657, 0.19862024]]]Python numpy ndarray array empty function
The empty function creates empty arrays. It is not always empty, and it might load garbage values or zeros, etc. So, don’t be surprised!.
np.empty(3) np.empty((2, 3)) np.empty((2, 4)) np.empty((2, 3, 5))
[3., 2., 1.]
[[4.33404091e-311, 1.97626258e-323, 1.20871698e-315],
[2.14187885e-296, 8.58539581e-210, 6.25613152e-309]]
[[-0.00000000e+000, 4.33404091e-311, 1.97626258e-323,
nan],
[ 1.20871698e-315, 2.14187885e-296, -8.58539581e-210,
6.25613152e-309]]
[[[-0.00000000e+000, -0.00000000e+000, -7.90505033e-323,
0.00000000e+000, 2.12199579e-314],
[ 0.00000000e+000, 0.00000000e+000, 0.00000000e+000,
1.77229088e-310, 3.50977866e+064],
[ 0.00000000e+000, 0.00000000e+000, nan,
nan, 3.50977942e+064]],
[[ 0.00000000e+000, -0.00000000e+000, -0.00000000e+000,
-3.95252517e-323, 0.00000000e+000],
[ 2.12199579e-314, 0.00000000e+000, 0.00000000e+000,
0.00000000e+000, 1.77229088e-310],
[ 3.50977866e+064, 0.00000000e+000, 0.00000000e+000,
nan, nan]]]Python numpy ndarray array full function
The full function creates the following one of a given number.
# Returns one dimensional of 4’s of size 5 np.full((5), 4) # Returns 3 * matrix of number 9 np.full((3, 4), 9) np.full((4, 4), 8) np.full((2, 3, 6), 7)
[4, 4, 4, 4, 4]
[[9, 9, 9, 9],
[9, 9, 9, 9],
[9, 9, 9, 9]]
[[8, 8, 8, 8],
[8, 8, 8, 8],
[8, 8, 8, 8],
[8, 8, 8, 8]]
[[[7, 7, 7, 7, 7, 7],
[7, 7, 7, 7, 7, 7],
[7, 7, 7, 7, 7, 7]],
[[7, 7, 7, 7, 7, 7],
[7, 7, 7, 7, 7, 7],
[7, 7, 7, 7, 7, 7]]]Python numpy ndarray identical array
The eye function creates an identical N * N matrix, where N is the given argument value.
print(np.eye(2)) print(np.eye(3)) print(np.eye(5))
[[1., 0.],
[0., 1.]]
[[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]]
[[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]]Python numpy ndarray diagonal array
The diag function is used in creating an identical, where diagonal values are filled with the list values.
np.diag([3]) np.diag([1, 2]) np.diag([1, 2, 3, 4]) np.diag([1, 2, 3, 4, 5, 6])
>>> np.diag([3])
[[3]]
>>> np.diag([1, 2])
[[1, 0],
[0, 2]]
>>> np.diag([1, 2, 3, 4])
[[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]]
>>> np.diag([1, 2, 3, 4, 5, 6])
[[1, 0, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 0],
[0, 0, 3, 0, 0, 0],
[0, 0, 0, 4, 0, 0],
[0, 0, 0, 0, 5, 0],
[0, 0, 0, 0, 0, 6]]Accessing Python numpy ndarray Array Items
We can access the individual elements using the index position. The index position always starts at 0 and ends at n-1, where n is the size, row size, or column size, or dimension. Access the items from one-dimensional.
arr = np.array([10, 15, 25, 35, 45, 55, 65]) arr arr[0] arr[2] arr[5] arr[7] arr[2:5]
The output of accessing the one-dimensional items
>>> arr = np.array([10, 15, 25, 35, 45, 55, 65])
>>> arr
array([10, 15, 25, 35, 45, 55, 65])
>>> arr[0]
10
>>> arr[2]
25
>>> arr[5]
55
>>> arr[7]
Traceback (most recent call last):
File "<pyshell#165>", line 1, in <module>
arr[7]
IndexError: index 7 is out of bounds for axis 0 with size 7
>>> arr[2:5]
array([25, 35, 45])As you can see, the last but one statement is throwing an error (index out of range) because n-1 (7-1) is the last index value we have. We used arr[2:5], which returns a portion of an array to view. It’s called slicing.
This example shows how to access two-dimensional items using indexes.
arr = np.array([[1, 2, 3, 4, 5],[12, 15, 61, 11, 19]]) arr[0][1] arr[0][4] arr[1][1] arr[1][4]
The output of accessing items
>>> import numpy as np
>>> arr = np.array([[1, 2, 3, 4, 5],[12, 15, 61, 11, 19]])
>>> arr
array([[ 1, 2, 3, 4, 5],
[12, 15, 61, 11, 19]])
>>> arr[0][1]
2
>>> arr[0][4]
5
>>> arr[1][1]
15
>>> arr[1][4]
19Alter Python numpy ndarray array Items
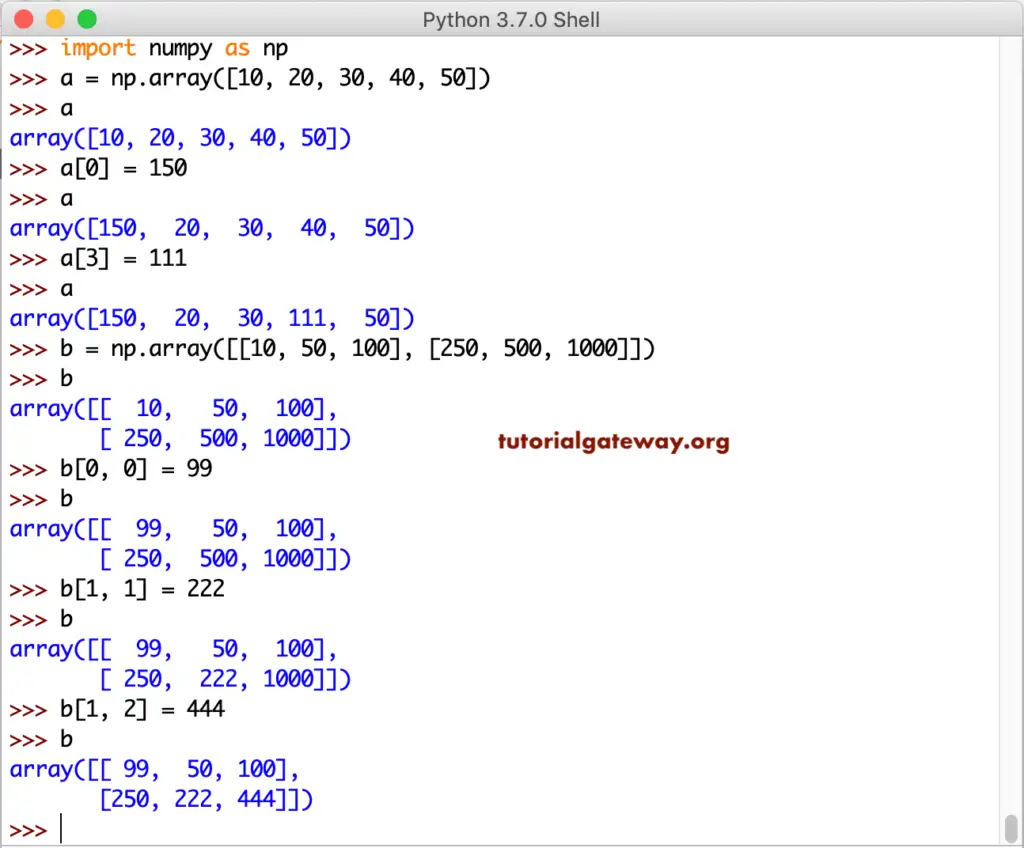
Same as accessing elements, you can alter one and two-dimensional items using the index position. It is an example of accessing the items from a one-dimensional.
a = np.array([10, 20, 30, 40, 50]) a a[0] = 150 a a[3] = 111 a b = np.array([[10, 50, 100], [250, 500, 1000]]) b b[0, 0] = 99 b b[1, 1] = 222 b b[1, 2] = 444 b
The output of altering the items
Python numpy ndarray Array Slicing
First, we declare a single or one-dimensional and slice that one. The slicing accepts an index position of the start and endpoint. The syntax of this is array_name[Start_poistion, end_posiition].
Both the start and end position has default values of 0 and n-1(maximum length). For example, arr1[1:5] means starts at index position 1 and ends at position 5. arr1[:7] starts at 0 and ends at index position 7.
One-dimensional slicing output
>>> arr1 = np.array([10, 25, 50, 75, 100, 125, 150, 200, 250])
>>> arr1
[ 10, 25, 50, 75, 100, 125, 150, 200, 250]
>>> arr1[1:5]
[ 25, 50, 75, 100]
>>> arr1[2:7]
[ 50, 75, 100, 125, 150]
>>> arr1[4:8]
[100, 125, 150, 200]
>>> arr1[3:9]
[ 75, 100, 125, 150, 200, 250]
>>> arr1[3:]
([ 75, 100, 125, 150, 200, 250]
>>> arr1[:7]
[ 10, 25, 50, 75, 100, 125, 150]This time, we declared a two-dimensional and sliced the same using index values.
arr2 = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
print(arr2)
print(arr2[:2, :2])
print(arr2[:3, :4])
print(arr2[:3, ])
print(arr2[:3])
print(arr2[:4])
print(arr2[:,:4])
slicing output
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]
[ 82 119 18 156 81]
[ 38 10 151 24 14]]
[[26 48]
[33 95]]
[[ 26 48 91 57]
[ 33 95 68 109]
[111 194 7 22]]
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]]
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]]
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]
[ 82 119 18 156 81]]
[[ 26 48 91 57]
[ 33 95 68 109]
[111 194 7 22]
[ 82 119 18 156]
[ 38 10 151 24]]Slicing ndarray with Negative Values
From the above examples, let me use the negative values as the start and end positions.
>>> arr1 = np.array([10, 25, 50, 75, 100, 125, 150, 200, 250])
>>> arr2 = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
>>> arr1[:3]
[10, 25, 50]
>>> arr1[:-4]
[ 10, 25, 50, 75, 100]
>>> arr1[-4:]
[125, 150, 200, 250]
>>> arr2[:-2, :-1]
[[ 26, 48, 91, 57],
[ 33, 95, 68, 109],
[111, 194, 7, 22]]
>>> arr2[:-3, :-1]
[[ 26, 48, 91, 57],
[ 33, 95, 68, 109]]
>>> arr2[:-3,]
[[ 26, 48, 91, 57, 120],
[ 33, 95, 68, 109, 155]]
>>> arr2[:,:-3]
[[ 26, 48],
[ 33, 95],
[111, 194],
[ 82, 119],
[ 38, 10]]
>>> arr2[:,:-2]
[[ 26, 48, 91],
[ 33, 95, 68],
[111, 194, 7],
[ 82, 119, 18],
[ 38, 10, 151]]Reverse Python numpy ndarray Array
Using the negative index value, you can reverse the rows and column position of values, which is called Numpy array reverse.
arr1 = np.array([10, 50, 100, 150, 250])
arr2 = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
print(arr1[::-1])
# Reverse the row position only
print(arr2[::-1,])
# Reverse both the row and column position
print(arr2[::-1, ::-1])
[250, 150, 100, 50, 10]
[[ 38, 10, 151, 24, 14],
[ 82, 119, 18, 156, 81],
[111, 194, 7, 22, 124],
[ 33, 95, 68, 109, 155],
[ 26, 48, 91, 57, 120]]
[[ 14, 24, 151, 10, 38],
[ 81, 156, 18, 119, 82],
[124, 22, 7, 194, 111],
[155, 109, 68, 95, 33],
[120, 57, 91, 48, 26]]Create an Array from existing
This example shows how to create an array from an existing one. For this, we are using the slicing concept.
Creating using the slicing technique output
>>> arr1 = np.array([10, 50, 100, 150, 250])
>>> arr2 = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
>>> arr3 = arr1[2:7]
>>> arr3
[100, 150, 250]
>>> arr4 = arr1[3:]
>>> arr4
[150, 250]
>>> arr5 = arr2[::-1,]
>>> arr5
[[ 38, 10, 151, 24, 14],
[ 82, 119, 18, 156, 81],
[111, 194, 7, 22, 124],
[ 33, 95, 68, 109, 155],
[ 26, 48, 91, 57, 120]]
>>> arr6 = arr2[::-1, ::-1]
>>> arr6
[[ 14, 24, 151, 10, 38],
[ 81, 156, 18, 119, 82],
[124, 22, 7, 194, 111],
[155, 109, 68, 95, 33],
[120, 57, 91, 48, 26]]Python Numpy ndarray array Boolean index
The array boolean index in Python Numpy ndarray object is an important part to notice. You can use this boolean index to check whether each item is in an array with a condition.
First, x = arr1 > 40 returns a boolean true and false based on the condition (arr1 > 40). I mean, if a value is greater than 40, True; otherwise, False. Next, arr1[x] returns an array of a sequence whose value is greater than 40. The same applies to multi-Dimensional.
arr1 = np.array([10, 20, 50, 90, 5, 40, 60, 30, 25])
x = arr1 > 40
print(arr1)
print(Bool index : ", x)
print(arr1[x])
y = arr1 < 40
print("\nBool index : ", y)
print(arr1[y])
arr2 = np.array(np.random.randint(1, 10, size = (3, 8)))
z = arr2 > 4
print("\n-----Arr2------\n", arr2)
print("------Bool index------\n", z)
print("------Arr2 of Z------\n", arr2[z])
[10 20 50 90 5 40 60 30 25]
Bool index : [False False True True False False True False False]
[50 90 60]
Bool index : [ True True False False True False False True True]
[10 20 5 30 25]
----- Arr2 ------
[[3 1 5 9 9 8 9 9]
[7 8 8 6 6 7 5 3]
[8 8 2 6 8 2 2 8]]
------ Bool index ------
[[False False True True True True True True]
[ True True True True True True True False]
[ True True False True True False False True]]
------ Arr2 of Z ------
[5 9 9 8 9 9 7 8 8 6 6 7 5 8 8 6 8 8]Replace infinity and NaN values in a Python numpy ndarray array
Replacing Not a Number and infinity values in a ndarray with exact numbers or values. Here, we declared 1D and 2D arrays with random values. Next, we replaced infinity and Nan with 11.56 and 29.16.
arr1 = np.array([10, 20, 50, 90, 5, 40, 60, 30, 25], dtype = 'float')
print(arr1)
arr1[2] = np.nan
arr1[4] = np.inf
print(arr1)
# Replace inf and nan With 11.56
x = np.isinf(arr1) | np.isnan(arr1)
arr1[x] = 11.56
print(arr1)
arr2 = np.array( [[9, 7, np.nan, 8, np.inf],
[np.nan, 3, 7, np.inf, 5],
[8, np.inf, 4, np.nan, 1]],
dtype = 'float')
print("\n-----------\n")
print( arr2)
# Replace inf and nan in arr2 With 29.16
y = np.isinf(arr2) | np.isnan(arr2)
arr2[y] = 29.16
print("\n-----------\n")
print(arr2)
The output of replacing NaN and Infinity values
[10. 20. 50. 90. 5. 40. 60. 30. 25.]
[10. 20. nan 90. inf 40. 60. 30. 25.]
[10. 20. 11.56 90. 11.56 40. 60. 30. 25. ]
-----------
[[ 9. 7. nan 8. inf]
[nan 3. 7. inf 5.]
[ 8. inf 4. nan 1.]]
------------
[[ 9. 7. 29.16 8. 29.16]
[29.16 3. 7. 29.16 5. ]
[ 8. 29.16 4. 29.16 1. ]]Arithmetic Operations on Python numpy ndarray Array
It allows you to perform arithmetic operations on one, two, and multi-dimensional using Arithmetic Operators. This example shows how to add, subtract, and multiply values on 1D, 2D, and multi-dimensional.
arr = np.array([10, 15, 25, 35, 45, 55, 65]) print(arr) print(arr + 4) print(arr - 8) print(arr * 3) two = np.array([[1, 2, 3, 4, 5],[12, 15, 61, 11, 19]]) print(two) print(two + 10) print(two - 3) print(two * 2) three = np.array([[1, 2, 3], [10, 20, 30], [6, 7, 8]]) print(three + 2) print(three - 5) print(three * 5)
[10 15 25 35 45 55 65]
[14 19 29 39 49 59 69]
[ 2 7 17 27 37 47 57]
[ 30 45 75 105 135 165 195]
[[ 1 2 3 4 5]
[12 15 61 11 19]]
[[11 12 13 14 15]
[22 25 71 21 29]]
[[-2 -1 0 1 2]
[ 9 12 58 8 16]]
[[ 2 4 6 8 10]
[ 24 30 122 22 38]]
[[ 3 4 5]
[12 22 32]
[ 8 9 10]]
[[-4 -3 -2]
[ 5 15 25]
[ 1 2 3]]
[[ 5 10 15]
[ 50 100 150]
[ 30 35 40]]Python numpy ndarray array Objects
The following attributes help to find the information about an array.
- ndim attribute: Returns the dimension. If it is a one-dimensional, then 1, two-dimensional = 2, etc.
- size: It displays or returns the number of elements or items.
- flags: Information about the memory layout.
- itemsize: Length in bytes.
- nbytes: Total number of bytes consumed it.
The following Python Numpy ndarray Array example shows the same.
a = np.array([10, 50, 100, 150, 250])
b = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[38, 10, 151, 24, 14]])
print('Dimension = ', a.ndim)
print('No of Elements = ', a.size)
print('Memory Layout = ', a.flags)
print('Length in Bytes = ', a.itemsize)
print('Total bytes consumed = ', a.nbytes)
print('\nDimension = ', b.ndim)
print('No of Elements = ', b.size)
print('Memory Layout = ', b.flags)
print('Length in Bytes = ', b.itemsize)
print('Total bytes consumed = ', b.nbytes)
Dimension = 1
No of Elements = 5
Memory Layout = C_CONTIGUOUS : True
F_CONTIGUOUS : True
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
UPDATEIFCOPY : False
Length in Bytes = 8
Total bytes consumed = 40
Dimension = 2
No of Elements = 25
Memory Layout = C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
UPDATEIFCOPY : False
Length in Bytes = 8
Total bytes consumed = 200Python numpy ndarray array shape
The ndarray shape object is useful to display the array shape precisely and dimensions.
- If it is one-dimensional, it returns the number of items.
- If it is 2D, it returns the rows and columns. Generally, it assigns a proper data type to the one that we create. However, the array function also allows you to specify the data type explicitly using dtype. Using this dtype object, either you can see the data type assigned to it implicitly or can assign your own type explicitly.
In this example, we created 1d, 2d, and three-dimensional. Next, we are using this shape object to return their matrix shapes.
arr1 = np.array([10, 50, 100, 150, 250])
arr2 = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
arr3 = np.array([[12, 11, 0, 9, 7], [10, 4, 11, 6, 9],
[9, 2, 10, 9, 11], [ 5, 14, 0, 11, 8]])
print("Arr 1. : ", arr1)
print("Arr 1 Shape : ", arr1.shape)
print("Arr 2 : \n", arr2)
print("Arr 2 Sp : ", arr2.shape)
print("Arr 3 : \n", arr3)
print("Arr 3 Sp : ", arr3.shape)
Arr 1. : [ 10 50 100 150 250]
Arr 1 Shape : (5,)
Arr 2 :
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]
[ 82 119 18 156 81]
[ 38 10 151 24 14]]
Arr 2 Sp : (5, 5)
Arr 3 :
[[12 11 0 9 7]
[10 4 11 6 9]
[ 9 2 10 9 11]
[ 5 14 0 11 8]]
Arr 3 Sp : (4, 5)Python numpy ndarray Array dtype
Generally, it assigns a proper data type that we create. However, this function also allows you to specify the data type of an array explicitly using dtype. Using this dtype, either you can see the data type assigned to it implicitly or can assign your own data type explicitly.
List of available data types to create a ndarray.
| Data Type | Description | Code |
|---|---|---|
| int8 | Signed 8 bit integer type | i1 |
| uint8 | Unsigned 8 bit integer type | u1 |
| int16, uint16 | Signed and Unsigned 16 bit integer types | i2, u2 |
| int32, uint32 | Signed & Unsigned 32 bit integer types | i4, u4 |
| int64, uint64 | Signed & Unsigned 64-bit integer types | i8, u8 |
| float16 | Half Precision floating point | f2 |
| float32 | Single Precision floating point | f4 or f |
| float64 | Double Precision float point | f8 or d |
| float128 | Extended Precision float point | f16 or g |
| complex64, complex128, complex256 | Complex numbers represented by 32, 64, 128 etc | c8, c16, c32 |
| bool | Boolean True or False Type | ? |
| object | Object Type | O |
| string_ | String type. You have to specify the string length (no of characters). For example, 5 characters mean S5 | S |
| unicode_ | Unicode Type. You have to specify the number of bytes. For example, 10 means U10. | U |
In this example, we are creating two ndarrays. First, we create an array of integers and mixed values (float and integer). Finally, we find their data types using dtype property.
arr1 = np.array([10, 20, 30, 40, 50])
print("Arr : ", arr1)
print("Type : ", arr1.dtype)
arr2 = np.array([1, 3.10, 4.60, 5, 7.96])
print("\nArr : ", arr2)
print("Type : ", arr2.dtype)
Arr : [10 20 30 40 50]
Type : int64
Arr : [1. 3.1 4.6 5. 7.96]
Type : float64The Numpy dtype property is not about finding the Array data type. We can use this property to create a ndarray of our own data types.
list1 = [10, 20, 30, 40, 50]
arr1 = np.array(list1, dtype = 'int')
print("Arr : ", arr1)
print("Type : ", arr1.dtype)
arr2 = np.array(list1, dtype = 'float')
print("Arr2 : ", arr2)
print("Type : ", arr2.dtype)
arr3 = np.array(list1, dtype = 'float16')
print("Arr3 : ", arr3)
print("Type : ", arr3.dtype)
Arr : [10 20 30 40 50]
Type : int64
Arr2 : [10. 20. 30. 40. 50.]
Type : float64
Arr3 : [10. 20. 30. 40. 50.]
Type : float16A few more examples to create an array of our own data type using dtype
list1 = [1, 20, 0, 40, 0]
arr1 = np.array(list1, dtype = 'S')
print("Arr1 : ", arr1)
print("Arr1Type : ", arr1.dtype)
arr2 = np.array(list1, dtype = 'bool')
print("Arr2 : ", arr2)
print("Arr2 Type : ", arr2.dtype)
arr3 = np.array([1, 10, 'e', 'o', 9, 'Hi', 7], dtype = 'object')
print("Arr3 : ", arr3)
print("Arr3 Type : ", arr3.dtype)
dtype properties output
Arr1 : [b'1' b'20' b'0' b'40' b'0']
Arr1 Type : |S2
Arr2 : [ True True False True False]
Arr2 Type : bool
Arr3 : [1 10 'e' 'o' 9 'Hi' 7]
Arr3 Type : objectreshape method
The Python numpy ndarray Array reshape function helps to reshape or change the size as per your requirement. Here, First, we are changing single dimensional to two-dimensional. Next, we changed the shape to 4 * 3, and 2 * 6.
arr1 = np.array([10, 20, 30, 40, 50, 60, 70, 80])
print("Arr : ", arr1)
x = arr1.reshape(2, 4)
print("------New Array 2 * 4------\n", x)
y = arr1.reshape(4, 2)
print("------New 4 * 2------\n", y)
arr2 = np.array( np.random.randint(1, 9, size = (3, 4)))
print("-----Arr2------\n", arr2)
a = arr2.reshape(4, 3)
print("------New Arr2 4 * 3------\n", a)
b = arr2.reshape(2, 6)
print("------New Arr2 2 * 6------\n", b)
Arr : [10 20 30 40 50 60 70 80]
------New Array 2 * 4------
[[10 20 30 40]
[50 60 70 80]]
------New 4 * 2------
[[10 20]
[30 40]
[50 60]
[70 80]]
-----Arr2------
[[6 2 5 5]
[8 6 2 1]
[4 3 1 8]]
------New Arr2 4 * 3------
[[6 2 5]
[5 8 6]
[2 1 4]
[3 1 8]]
------New Arr2 2 * 6------
[[6 2 5 5 8 6]
[2 1 4 3 1 8]]Python numpy ndarray Array flatten and ravel
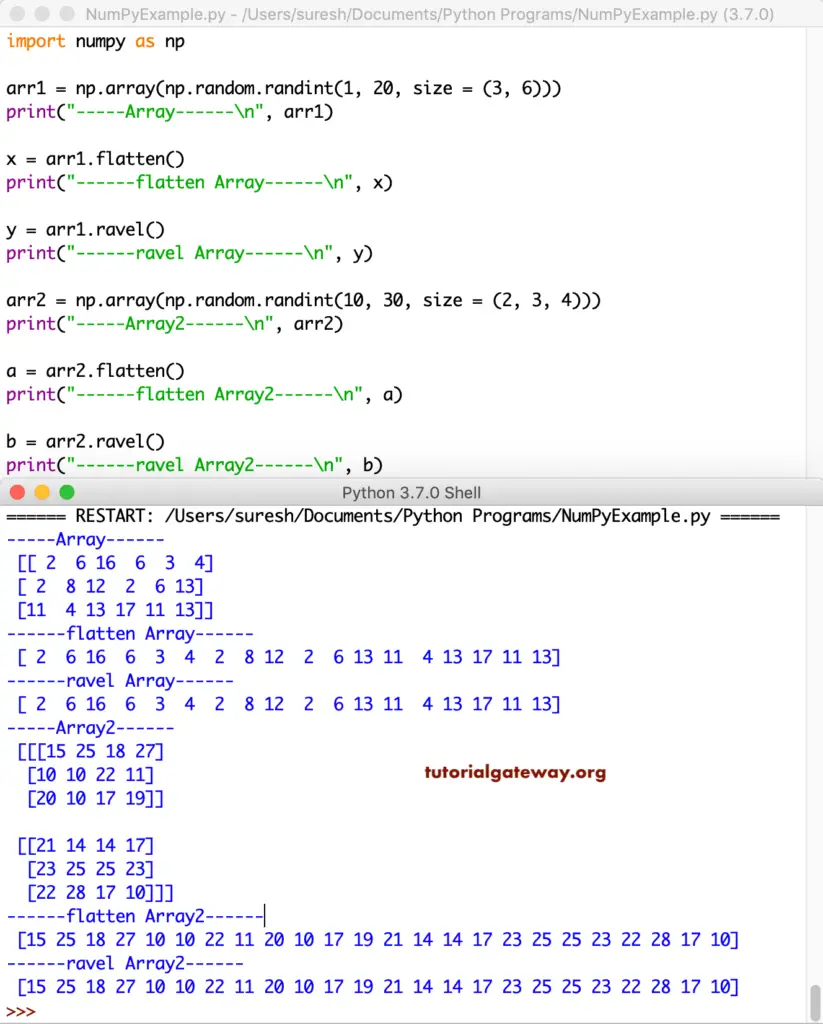
Both flattens, and ravel methods flatten or convert any size to a single dimensional. Although both are the same, the ravel holds the reference of an actual one. It means any changes made to the ravel output also reflect the original array. However, this is not the same as the flatten.
arr1 = np.array(np.random.randint(1, 20, size = (3, 6)))
print("-----Arr------\n", arr1)
x = arr1.flatten()
print("------flatten------\n", x)
y = arr1.ravel()
print("------ravel------\n", y)
arr2 = np.array(np.random.randint(10, 30, size = (2, 3, 4)))
print("-----2nd------\n", arr2)
a = arr2.flatten()
print("------flatten 2------\n", a)
b = arr2.ravel()
print("------ravel 2------\n", b)
flatten and ravel method output
How to find Unique Items in a Python numpy ndarray array?
This module has a unique method that is used to find and return the unique values from a given 1D, 2D, and 3 or multi Dimensional.
arr = np.random.randint(0, 5, size = 10)
print('Original = ', arr)
uniq = np.unique(arr)
print('Unique Items = ', uniq)
arr2 = np.random.randint(10, 100, size = (3, 5))
print('\n---2D Rand Original ----\n', arr2)
uniq2 = np.unique(arr2)
print('Unique Items = ', uniq2)
arr3 = np.random.randint(15, 25, size = (2, 3, 8))
print('\n----Three Dimensional Rand Original ----\n', arr3)
uniq3 = np.unique(arr3)
print('Unique Items = ', uniq3)
Original = [0 3 4 3 0 4 4 0 0 0]
Unique Items = [0 3 4]
---2D Rand Original ----
[[73 98 42 59 96]
[97 86 20 69 52]
[91 98 76 48 41]]
Unique Items = [20 41 42 48 52 59 69 73 76 86 91 96 97 98]
----Three Dimensional Rand Original ----
[[[19 21 19 24 19 15 20 20]
[24 20 19 19 21 21 16 17]
[22 23 23 16 23 20 18 17]]
[[24 23 23 21 18 19 17 21]
[15 21 22 18 16 17 24 23]
[17 15 21 19 20 15 15 15]]]
Unique Items = [15 16 17 18 19 20 21 22 23 24]Count unique items
Count the total number of times each item is repeated in an array. For this, you have to use the unique method with the return_counts parameter. If we set this parameter value to True, then it counts items.
arr = np.random.randint(0, 5, size = 10)
print('Original = ', arr)
uniq, cnt = np.unique(arr, return_counts = True)
print('Unique Items = ', uniq)
print('Count Items = ', cnt)
arr2 = np.random.randint(10, 100, size = (3, 5))
print('\n---2D Random Original ----\n', arr2)
uniq2, cnt2 = np.unique(arr2, return_counts = True)
print('Unique Items = ', uniq2)
print('Count Items = ', cnt2)
arr3 = np.random.randint(15, 25, size = (2, 3, 8))
print('\n----Three Dimensional Random Original ----\n', arr3)
uniq3, cnt3 = np.unique(arr3, return_counts = True)
print('Unique Items = ', uniq3)
print('Count Items = ', cnt3)
Original = [0 1 1 0 2 4 2 3 4 0]
Unique Items = [0 1 2 3 4]
Count Items = [3 2 2 1 2]
---2D Random Original----
[[47 25 28 61 23]
[78 15 75 77 98]
[31 58 94 99 15]]
Unique Items = [15 23 25 28 31 47 58 61 75 77 78 94 98 99]
Count Items = [2 1 1 1 1 1 1 1 1 1 1 1 1 1]
----Three Dimensional Random Original ----
[[[17 16 18 20 18 24 20 22]
[24 22 17 17 19 18 18 21]
[15 19 19 18 16 24 19 21]]
[[24 16 16 24 24 16 19 19]
[17 15 17 15 15 17 23 20]
[22 15 24 16 21 22 24 22]]]
Unique Items = [15 16 17 18 19 20 21 22 23 24]
Count Items = [5 6 6 5 6 3 3 5 1 8]Python Numpy ndarray Array Transpose
In Python, we have T and transpose functions to transpose a matrix or an array. Transpose means rows converted to columns, and columns converted to rows.
import numpy as np
a = np.array([[26, 48, 91, 57, 120], [33, 95, 68, 109, 155],
[111, 194, 7, 22, 124], [ 82, 119, 18, 156, 81],
[ 38, 10, 151, 24, 14]])
b = np.array([[12, 11, 0, 9, 7], [10, 4, 11, 6, 9],
[ 9, 2, 10, 9, 11], [ 5, 14, 0, 11, 8]])
print('Original')
print(a)
print('\nTransposed ')
print(a.T)
print('\nOriginal')
print(b)
print('\nTransposed')
print(np.transpose(b))
Original
[[ 26 48 91 57 120]
[ 33 95 68 109 155]
[111 194 7 22 124]
[ 82 119 18 156 81]
[ 38 10 151 24 14]]
Transposed
[[ 26 33 111 82 38]
[ 48 95 194 119 10]
[ 91 68 7 18 151]
[ 57 109 22 156 24]
[120 155 124 81 14]]
Original
[[12 11 0 9 7]
[10 4 11 6 9]
[ 9 2 10 9 11]
[ 5 14 0 11 8]]
Transposed
[[12 10 9 5]
[11 4 2 14]
[ 0 11 10 0]
[ 9 6 9 11]
[ 7 9 11 8]]Built-in Functions
Python NumPy has many built-in ndarray functions to work with arrays. We have already explained all these methods with examples in the regular Tutorial.
| Operators | List of Functions and Operators |
|---|---|
| Arithmetic Operators | +, -, *, / |
| Arithmetic Methods | add, subtract, multiply, divide, mod, the remainder |
| Aggregate | sum, average, prod, min, max, maximum, minimum, mean, median, var, std, cumsum, cumprod, percentile, argmin, argmax, corrcoef |
| Bitwise Operators | &, |, ~, ^, left_shift, right_shift |
| Bitwise Methods | bitwise_and, bitwise_or, bitwise_not, bitwise_xor |
| Comparison Operators | <, <=, ==, <, >=, != |
| Comparison methods | equal, less, less_equal, greater, greater_equal, not_equal |
| Logical Operators | and, or, not |
| Logical methods | logical_and, logical_or, logical_not, logical_xor |
| Exponential | exp, exp2, expm1, log, log2, log10, log1p, logspace |
| Mathematical | The list of mathematical methods are abs, ceil, floor, mod, modf, round, sinc, sign, trunc, square, reciprocal, power, sqrt, cbrt |
| String Functions | add, multiply, capitalize, title upper, lower, center, split, splitlines, strip, join, replace, encode, and decode. |
| Trigonometric | sin, cos, tan, arcsin, arccos, arctan, arctan2, radians, degrees, hypot, deg2rad, rad2deg, unwrap |
| Hyperbolic | sinh, acsinh, cosh, arccosh, tanh, atctanh |
| Predicates | isfinite, isinf, isnan, signbit, digitize, tile |
