Recursion in C programming is a powerful technique that lets a function call itself within its own body to solve problems. Similar to loops, it performs the repetitive process by calling the same function with different (updated) values until the base condition is met.
This programming language introduced a new technique called Recursion for simple and elegant coding. Recursion in C langauge languageis useful for calling the same function one or more times. Apart from that, we can use recursion to divide a large problem into smaller ones, solve those small problems in parallel, and combine the results as the final output.
This article will show you the syntax, types of recursion, and how to write a program using Recursion in C Programming with a practical example.
C Recursion syntax
The syntax of the recursion depends upon the type that you choose. However, the default or basic syntax to explain the recursion process is shown below.
return_type function_name(value)
{
// Base Case
if(base_condition) {
return Value;
}
// Recursive Case
return function_name(updated_Value)
}
From the above recursion syntax,
- Return type: The type of value this function will return. It can be void() for the printf() statement, int for integers, double, char, etc.
- function_name: The name of the function.
- Value: A C recursive function allows one or two parameter values. If it is two arguments, the second one will save the intermediate results.
We can divide the body of the recursive function into two parts:
- Base case: Condition to end the recursive calls. In the above syntax, base_condition is the base case.
- Recursive case: Calling the function itself with updated values. In the above syntax, function_name(updated_Value) is the recursive case.
How C Recursion Works?
Once the compiler enters a recursive function, it will continue until it meets a certain condition to stop. So, in general, we use the if statement for the base condition or If else statement to execute the base condition and recursive call.
Base Case
In this section, we must specify a condition that stops the C recursion. Basically, the base condition instructs the compiler to stop performing the recursions and exit the function. If you miss the base condition, it will lead to calling itself forever (infinitely).
Recursive Case
This is the section where we recursively call the function itself one or more times based on the recursion type. When calling the function itself, we must pass the updated parameter value as an argument. The updated value can be smaller than the original, and after a few recursion cycles, it will end up matching the base condition. So, the recursion process stops.
If you call the function without updating the value, it will call the same function infinite times, leading to a stack overflow. For example, calling main() from the main() function.
NOTE: If you miss the base condition or recursive calling to a function with the same value (without updating), it leads to inifinite loop.
We use the above C recursion syntax to explain the working functionality of the recursion.
- Step 1: From the main() function, we call the recursive function with a default value. For instance, 3.
- Step 2: When a function is called from the main(), the compiler jumps into the function_name with 3 as the parameter value.
- Step 3: The function checks whether the base condition is True. If True, don’t go further. Execute the code inside the base condition block and exit from the function.
- Step 4: If the base condition is False, it will call the function itself with an updated value, maybe 2. It adds a new call to the stack with 2.
- Step 5: Again, check the base condition. If false, call the function again. It repeats until the base condition is True.
NOTE: Every new recursive function call is added to the stack, and the new call is pushed to the top. Once the base condition is met, it starts completing the stacks.
Types of Recursion in C
A recursion in C programming language is not about performing a single task by calling the same function repeatedly. We can use recursion to divide big problems into smaller parts, and traverse through a tree with nodes and sub-nodes. To understand them better, the recursions are divided into the following types.
Direct Recursion in C
It is the most common way of recursively calling a function. When a function directly calls itself within its own body with updated values, it is a direct recursion.
The direct recursion involves one or more recursive calls to the original function. The syntax of the direct recursion is
return_type function_name(parameters)
{
if(base_condition) {
return Value;
}
return function_name(updated_parameters_value)
}
In the above direct recursion syntax, the base_condition stops the C recursion process. When the condition is met, the direct recursion process will end. Next, the return statement directly calls the original function with an updated value (smaller or larger).
Direct Recursion Example
In the example below, we used the direct recursion in C programming approach to print the natural numbers in reverse order (from N to 1). Here, printingNumbers(n – 1) line calls the original function with a smaller number directly until it reaches 0. Once it reaches 0, the base condition will stop the iterations.
#include<stdio.h>
void printingNumbers(int n)
{
if(n == 0)
return;
else{
printf("%d ", n);
printingNumbers(n - 1);
}
}
int main()
{
printingNumbers(10);
}
10 9 8 7 6 5 4 3 2 1NOTE: The most famous direct recursion program is the Fibonacci series program, where we directly call the function itself multiple times. Please refer to the examples section to see the steps to print the Fibonacci series.
Indirect Recursion in C
Unlike direct recursion, indirect recursion is recursively calling one function from another in a circular manner to perform a certain operation. For instance, when multiple operations have to be performed recursively and independently. We will create multiple functions to perform those operations. When one function result depends on another function, we can call that function, called as the indirect recursion. For instance, Function A calls B, and B calls A or C.
The syntax of the indirect recursion in C programming is
return_type function1(parameters)
{
if(base_condition) {
return Value;
}
return function2(updated_parameters_value)
}
return_type function2(parameters)
{
if(base_condition) {
return Value;
}
return function1(updated_parameters_value)
}
In the above syntax, the return statement in the first function calls the second function (function2) with an updated parameter value. The second function calls function1 with an updated value.
We can say, indirect recursion is like a team work (work sharing) where one function is busy or unable to handle the job, forward it to the second function, third, etc.
Indirect Recursion Example
To explain the indirect recession in C in simple terms, imagine an organization has two employees. Many tasks should be completed daily. So, there should be work sharing between the two employees. In real-time, it may be done based on the task execution process, difficulty, etc. However, to make it simple, we want to share the even-number tasks with the first employee and the odd-number tasks with the second employee.
In the example below, the main() function calls the first employee. When the task is even, it will execute. If the task number is odd, it will call the second employee to execute that task.
#include <stdio.h>
void firstEmployee(int tasks);
void secondEmployee(int tasks);
void firstEmployee(int tasks) {
if(tasks <= 0) {
printf("Work Completed");
return;
}
if(tasks % 2 == 0) {
printf("First Employee Received Task %d and Processed it.\n", tasks);
secondEmployee(tasks - 1);
}
else {
printf("First Employee Received Task %d and Passed to Second\n", tasks);
secondEmployee(tasks);
}
}
void secondEmployee(int tasks) {
if(tasks <= 0) {
printf("Work Completed");
return;
}
if(tasks % 2 != 0) {
printf("Second Employee Received Task %d and Processed it.\n", tasks);
firstEmployee(tasks - 1);
}
else {
printf("Second Employee Received Task %d and Passed to First\n", tasks);
firstEmployee(tasks);
}
}
int main()
{
firstEmployee(7);
}
Result
First Employee Received Task 7 and Passed to Second
Second Employee Received Task 7 and Processed it.
First Employee Received Task 6 and Processed it.
Second Employee Received Task 5 and Processed it.
First Employee Received Task 4 and Processed it.
Second Employee Received Task 3 and Processed it.
First Employee Received Task 2 and Processed it.
Second Employee Received Task 1 and Processed it.
Work CompletedLinear Recursion in C
A linear recursion means that a function calls itself exactly once within its own body. Unlike direct recursion, where we can call the function directly more than once. The linear recursion is recursively calling itself for one and only once with updated values.
The syntax of the linear recursion in C language is shown below. As you can see, we call the original function only once within its body.
return_type function_name(parameters)
{
if(base_condition) {
return Value;
}
else {
return function_name(updated_parameter)
}
Linear Recursion Example
In the example below, we used the linear recursion concept to calculate the sum of individual digits in a given number. Here, the if statement inside the function is a base condition to stop the C recursive function calls when the number is zero.
Inside the else block, we call the digitsSum() function recursively with an updated value by removing one digit from the number.
#include <stdio.h>
int digitsSum(int n)
{
if(n == 0)
return 0;
else
return (n % 10) + digitsSum(n / 10);
}
int main()
{
int number = 4567;
printf("%d", digitsSum(number));
}
22If you observe the execution process, the program recursively calls digitsSum() until it becomes 0.
digitsSum(4567)
- 7 + digitsSum(456)
- 7 + 6 + digitsSum(45)
- 7 + 6 + 5 + digitsSum(4)
- 7 + 6 + 5 + 4 + digitsSum(0)
- 7 + 6 + 5 + 4 + 0 = 22
NOTE: The most famous linear recursion (not a direct recursion) program is finding the factorial of a number or the sum of natural numbers. Please refer to the examples section to see the steps to find the factorial.
Tail Recursion in C
A tail recursion means that within the function body, recursive calling of itself is the last operation performed. It means there should be nothing (no operations) executed, not even a printf statement used after the recursive function call. The last line should be the recursive calling of the function itself.
TIP: The tail recursion can be optimized by the compiler and uses less memory compared to the non-tail recursions. It is faster and safer than non-tail recursions.
When you want to perform certain actions before recursively calling the function with updated values, use tail recursion. The syntax of the tail recursion in C programming is
return_type function_name(parameters, accumulator)
{
if(base_condition) {
return accumulator;
}
return function_name(updated_parameter, updated_accumulator)
}
In the above syntax, the tail recursion accepts two parameters. Here, the accumulator stores the intermediate value for each recursive function call.
Tail Recursion Example
As it is easy to explain the C trail recursion and understandable, we use the same sum of digits program that we mentioned in the linear recursion section.
In the example below, total is the accumulator that stores the intermediate result, meaning the sum of digits on each iteration.
#include <stdio.h>
int digitsSum(int n, int total)
{
if(n == 0)
return total;
return digitsSum(n / 10, total + (n % 10));
}
int main()
{
int number = 3968;
printf("%d", digitsSum(number, 0));
}
26Analysis
digitsSum(3968, 0)
- digitsSum(396, 8)
- digitsSum(39, 14)
- digitsSum(3, 23)
- digitsSum(0, 26) = 26
Head Recursion in C
As the name suggests, the head recursion is a process where the recursive calling of a function itself happens first, and then the remaining work happens. Unlike tail recursion, where the recursive function calling is the last operation, head recursion calls the recursion first and then performs other operations.
As there are things that occur after recursively calling the function itself, it must wait until the completion of the remaining work. When we want to traverse the structure or numbers from bottom to top, we use the head recursion.
The syntax of the head recursion in C programming is
return_type function_name(parameters)
{
if(base_condition) {
return accumulator;
}
return function_name(updated_parameter)
// perform other operations
}
In the above syntax, after the head recursion execution, there are some operations that can be performed. Something like printing statements or calculating something.
Head Recursion Example
In the example below, we use the head recursion in C to print the natural numbers from 1 to n. Here, NumbersinAsc(n – 1) line recursively calls the original function first. Next, the printf() statement prints the value. Here, the compiler has to wait until the printf() statement completes.
#include<stdio.h>
void NumbersinAsc(int n)
{
if(n == 0)
return;
NumbersinAsc(n - 1);
printf("%d ", n);
}
int main()
{
NumbersinAsc(5);
}
1 2 3 4 5Mutual Recursion in C
A mutual recursion means that two functions circularly call each other. For example, function A calls B, and B calls A, which is an example of mutual recursion.
When there is a need to split calculations or tasks for parallel processing under different conditions. One task calls the other function from its own body, and the second function calls the first function from its own body. The syntax of the mutual recursion in C programming language is
return_type function1(parameters)
{
if(base_condition)
return Value;
return function2(updated_parameters)
}
return_type function2(parameters)
{
if(base_condition)
return Value;
return function1(updated_parameters)
}
In the above mutual recursion syntax, the return statement in the first function calls the second function (function2) with an updated parameter value. The second function calls function1 with an updated value. A-> B-> A.
Mutual Recursion Example
In the mutual recursion in C example below, within the body of the firstEmployee(), it calls the secondEmployee() with one number less than the actual task’s value. Similarly, within the secondEmployee() function, it calls firstEmployee() with update value.
Inside the main() function, it checks whether the given number is even or odd. If it is an even task, the first employee executes that task. When it is an odd task, the second employee executes the odd task.
#include <stdio.h>
void firstEmployee(int tasks);
void secondEmployee(int tasks);
void firstEmployee(int tasks)
{
if (tasks <= 0)
return;
printf("First Employee Processed Task %d.\n", tasks);
secondEmployee(tasks - 1);
}
void secondEmployee(int tasks)
{
if (tasks <= 0)
return;
printf("Second Employee Processed Task %d.\n", tasks);
firstEmployee(tasks - 1);
}
int main()
{
int n = 6;
if (n % 2 == 0)
{
firstEmployee(n);
}
else
{
secondEmployee(n);
}
}
Result
First Employee Processed Task 6.
Second Employee Processed Task 5.
First Employee Processed Task 4.
Second Employee Processed Task 3.
First Employee Processed Task 2.
Second Employee Processed Task 1.TIP: Every mutual recursion is an indirect recursion. However, every indirect recursion may not be mutual. For instance,
- Indirect means A -> B -> C -> A
- Mutual means A <-> B
Binary Recursion in C
A Binary recursion is a unique type where a function makes two recursive calls to itself within the same body during every execution. Unlike linear recursion, it splits the process into two equal parts and traverses each part to get the final result.
NOTE: The Fibonacci Series is a classic Binary recursion example. As we have explained in the examples section, please view it for better understanding.
The syntax of the Binary recursion in C programming for the divide and conquer approach is
return_type function_name(parameters)
{
if(base_condition)
return Value;
return function_name(part1) + function_name(part1)
}
As you can see from the above syntax, a function must contain two recursive calls to the same function with updated values. Here, part 1 traverses to the left side of the binary tree and part 2 traverses to the right side of the binary tree.
Binary Recursion Example
In the Binary recursion in C programming example below, within the totalcalls() function, we call the same function for two times within its body. Here, the return statement recursively calls the totalcalls() function for two times with one number smaller than the existing value.
#include <stdio.h>
int totalCalls(int n)
{
if (n == 0)
return 1;
return totalCalls(n - 1) + totalCalls(n - 1);
}
int main()
{
printf("%d", totalCalls(3));
}
8Here, the execution process follows the binary tree process. On each C recursive call, it creates a new branch until it reaches 0. When it reaches 0, the base condition returns 1 and exits the recursion process.
In the first iteration, n = 3, it splits into two. To make it easy, we consider the totalCalls() function name as f().
f(3) = f(2)) (Left) + f(2)) (Right)
On the second recursive call, n = 2 means the left side will split into two
- Left f(2) -> f(1) + f(1).
- Right f(2) -> f(1) + f(1).
On the next recursive call, the n value is 1, which means expand each f(1) with left and right branches with f(0). In the above, there are 4 f(1), and each f(1) splits into left and right. So, there are a total of 8 branches with f(0). As n becomes 0, the base condition stops iterations.
Tree Recursion in C
As the name suggests, a tree recursion forms a tree-like structure to perform the operations. The tree recursion allows a function to call itself recursively two or more times to split the problem.
A tree recursion helps explore all possible options and test more than one outcome. Something like permutations and combinations. The syntax of the Tree Recursion in C programming is shown below.
return_type function_name(parameters)
{
if(base_condition)
return Value;
return function_name(parameters - 1)
return function_name(parameters - 2)
}
As you can see from the above tree recursion, we can recursively call the function itself two or more times with updated values.
Tree Recursion Example
The example below is a basic example to demonstrate Tree recursion in C, and to make it more appealing, we performed the addition. If you remove n before the treeTotal(n / 2), it will split the given number into two equal parts and move towards the branches.
On each execution, it splits the number into two equal parts and moves to sub-branches and nested branches. It goes deep until it reaches 2. If it finds 1, the base condition executes and terminates the iterations for that branch.
#include <stdio.h>
int treeTotal(int n)
{
if (n <= 1)
return n;
return n + treeTotal(n / 2) + treeTotal(n - n / 2);
}
int main()
{
printf("%d", treeTotal(5));
}
17The given number is 5, and the C recursion function splits into two equal parts.
n + treeTotal(n / 2) + treeTotal(n – n / 2);
- 5 divides in to 2 and 3. It means 5 + f(2) + f(3). Let’s keep the main root value aside and work on the right and left side branches.
- On the left side, 2 divides into 1 and 1. It means, 2 + f(1) + f(1).
- On the left side, n becomes 1 for each tree branch, so there is no further splitting because of the base condition. So, the left side, 2 + 1 + 1 = 4.
- On the right side, 3 divides into 1 and 2. It means, 3 + f(1) + f(2).
- On the right side, f(2) further splits into two f(1) and f(1). So, there will be no next splitting because all branches become 1. So the right side result is 3 + 1 + 2 + 1 + 1 = 8.
- Total = 5 + 4 (left) + 8 (right) = 17.
C Recursion Examples
The following are some examples using recursion. Please refer to the C Programs page to see more examples using recursion.
Calculate factorial using Recursion in C
Let us consider a well-known simple example of calculating the factorial of a number to understand recursion.
5! = 5 * 4 * 3 * 2 * 1
We can calculate the factorial of any given number using the formula below.
n! = (n) * (n-1) * (n-2) * ….. * 1.
In C programming, we can achieve the output in multiple ways, such as using a for loop or a while loop. If you observe the above pattern, it is repetitive behaviour, meaning direct recursion. So instead of writing the loops, we can write the function using recursion.
#include <stdio.h>
int factorial(int n)
{
if (n == 0)
{
return 1;
}
return n * factorial(n - 1);
}
int main()
{
printf("%d", factorial(5));
}
120When we call the C recursion function from the main(), if the given Number is 0, the function will return 1. It is the base condition to stop the iterations. Otherwise, it will return the following line.
n * factorial(n – 1);
Let us calculate the factorial of 5!
5! = 5 * factorial(4); //(5 – 1) Calling the above function
= 5 * 4 * factorial (3) //(4 -1)
= 5 * 4 * 3 * factorial (2) // (3 -1)
= 5 * 4 * 3 * 2 * factorial (1) //(2 -1)
= 5 * 4 * 3 * 2 * 1 * 1 (base condition)
= 120
NOTE: Please refer to the C Program to find the Factorial of a Number article for further understanding.
Use C recursion to find the sum of Series 1²+2²+3²+… +n²
This program allows the user to enter the value of N. Then, this program will find the sum of the series using recursion or recursive functions.
#include <stdio.h>
int Sum_Of_Series(int);
int main()
{
int Number, Sum;
printf("\nPlease Enter any positive integer \n");
scanf("%d",&Number);
Sum=Sum_Of_Series(Number);
printf("\nSum of the Series = %d",Sum);
}
int Sum_Of_Series(int Number)
{
if(Number == 0)
return 0;
else
return (Number*Number) + Sum_Of_Series(Number-1);
}
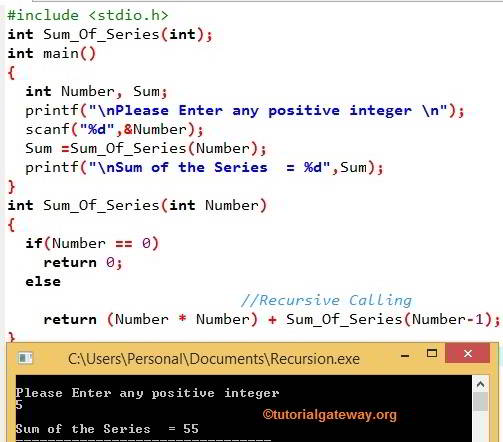
In this Recursion example, the first line of the program is the declaration of the User Defined Function. Within the C Programming main() function, We declared 2 integer variables.
The next printf statement will ask the user to enter any integer value. And the below scanf statement will assign the user integer value to the variable name Number.
In the next line, we called the user-defined function Sum_Of_Series() and assigned it to the integer variable Sum. When the compiler reaches the function call, it will jump to the function definition for the calculations.
C Recursion Function Definition
Within the Sum_Of_Series (Number) function, we used this Recursion. If the user enters the Number 0, the function will return 0. Else, it will return. It is called function Recursion in C programming.
(Number*Number) + Sum_Of_Series (Number-1);
Let us divide the above Recursion expression for a better understanding
(Number * Number) = Multiplying the number
Sum_Of_Series(Number-1) = Calling the same function with 1 number minus.
In this example program, the User entered value is 5:
Recursion 1: Number = 5, which is Greater than 0
Sum = (5 * 5) + Sum_Of_Series (5 – 1)
Sum = 25 + Sum_Of_Series (4)
2nd: Number = 4, which is Greater than 0, and Sum is 25
Sum = (4 * 4) + Sum_Of_Series (4 – 1)
Sum = 16 + Sum_Of_Series (3)
The sum value is: 25 +16 = 41
3rd Iteration of C recursion example: Number = 3, which is Greater than 0, and Sum is 41
Sum = (3 * 3) + Sum_Of_Series (3 – 1)
Sum = 9 + Sum_Of_Series (2) => 41 + 9 = 50
4th: Number = 2, which is Greater than 0, and Sum is 50
Sum = (2 * 2) + Sum_Of_Series (2 – 1)
Sum = 4 + 50 = 54
5th round of the recursion Iteration: Number = 1, which is Greater than 0, and Sum is 54
Sum = (1 * 1) + Sum_Of_Series (1 – 1) => 1 + Sum_Of_Series (0)
Sum value is: 54 + 1 = 55
rotation 6: Number = 0, which means the First if condition is True so that it will exit from it. The final value is 55
The final output of this C Recursion program = 55. We must use some sort of condition to exit the recursive function calls. If you forget the condition, the function will execute infinite times. Please refer to For Loop and While Loop articles.
Use C recursion to calculate the sum of natural numbers
In the example below, the base condition stops when the n becomes 0. The return statement adds each value and recursively calls the original function with the previous number. For instance, n = 10 means,
- 10 + total(9)
- 10 + 9 + total(8)
#include<stdio.h>
int total(int n)
{
if(n == 0)
return 0;
return n + total(n - 1);
}
int main()
{
printf("%d", total(10));
}
55NOTE: Please refer to the C Program to find the Sum of Natural Numbers from 1 to N article for further understanding.
Fibonacci Series using Recursion in C
The example below recursively calls the function itself multiple times to print the Fibonacci series numbers from 1 to 10.
#include <stdio.h>
int fibo(int n)
{
if (n <= 1)
return n;
return fibo(n -1) + fibo(n - 2);
}
int main()
{
int n = 10;
for(int i = 0; i < n; i++)
{
printf("%d ", fibo(i));
}
}
0 1 1 2 3 5 8 13 21 34NOTE: Please refer to the C Program to Print Fibonacci Series Numbers article for further understanding.
Use C recursion to calculate the GCD of two numbers
The example below directly calls the function itself recursively with the updated value to find the GCD (Greatest Common Divisor) of two numbers.
#include <stdio.h>
int findgcd(int a, int b)
{
if (b == 0)
return a;
return findgcd(b, a % b);
}
int main()
{
int a = 12, b = 18;
printf("%d ", findgcd(a, b));
}
6NOTE: Please refer to the C Program to Find the GCD of Two Numbers article for further understanding.
Use C recursion to reverse a string
In the example below, we used the head recursion to perform the string reverse. Here, after recursively calling the function itself with the updated value, there is a printf() statement to print the characters.
#include <stdio.h>
void rev(char str[], int i)
{
if (str[i] == '\0')
return;
rev(str, i + 1);
printf("%c", str[i]);
}
int main()
{
char s[] = "Hello";
rev(s, 0);
}
olleHNOTE: Please refer to the C Program to Reverse a String article for further understanding.
What is Stack Overflow in Recursion?
When performing the recursion in C language, we must be careful with stack overflow. It creates a stack memory when we call a recursive function from the main(), to store local variables and the recursive calls.
As we mentioned earlier, when there is a new recursive call to a function, it will add to the stack. In general, the base condition helps to stop the recursion, and when the compiler leaves the function, the stack memory disappears. However, if there are many recursive calls, it can lead to a stack overflow.
To demonstrate the stack overflow in the C recursion, we use the same factorial program that we mentioned in the examples section. However, we will calculate the factorial of 10000.
#include <stdio.h>
int fact(int n)
{
if (n == 0)
return 1;
return n * fact(n - 1);
}
int main()
{
printf("%d", fact(10000));
}
0If you observe the above output, it returns 0 instead of calculating the factorial. Here, the program must recursively call the original fact() function for 9999 times. Storing these many calls inside a stack memory leads to memory leaks or overflow.
Difference between C Recursion and Iteration
Both recursion and iteration are processes of repeating certain steps (executing a code) over and over until a certain condition is met. For simple operations like calculating the factorial, we can use the iteration approach, which needs less memory compared to recursion.
- Iteration is a process of using the For loop, While loop, and Do While loop to perform or execute a certain task until the loop condition is True. Once the condition fails, the compiler exits the loop and executes the next line of code.
- C Recursion is a process of calling the same function repeatedly with an updated value. Here, the recursive calling of a function may be once, twice, or from another function.
NOTE: Use iteration to perform calculations or execute a certain code. On the other hand, use recursion to distribute the code complexity to multiple functions that can work independently or interdependently.