Go Program to Check Identity Matrix

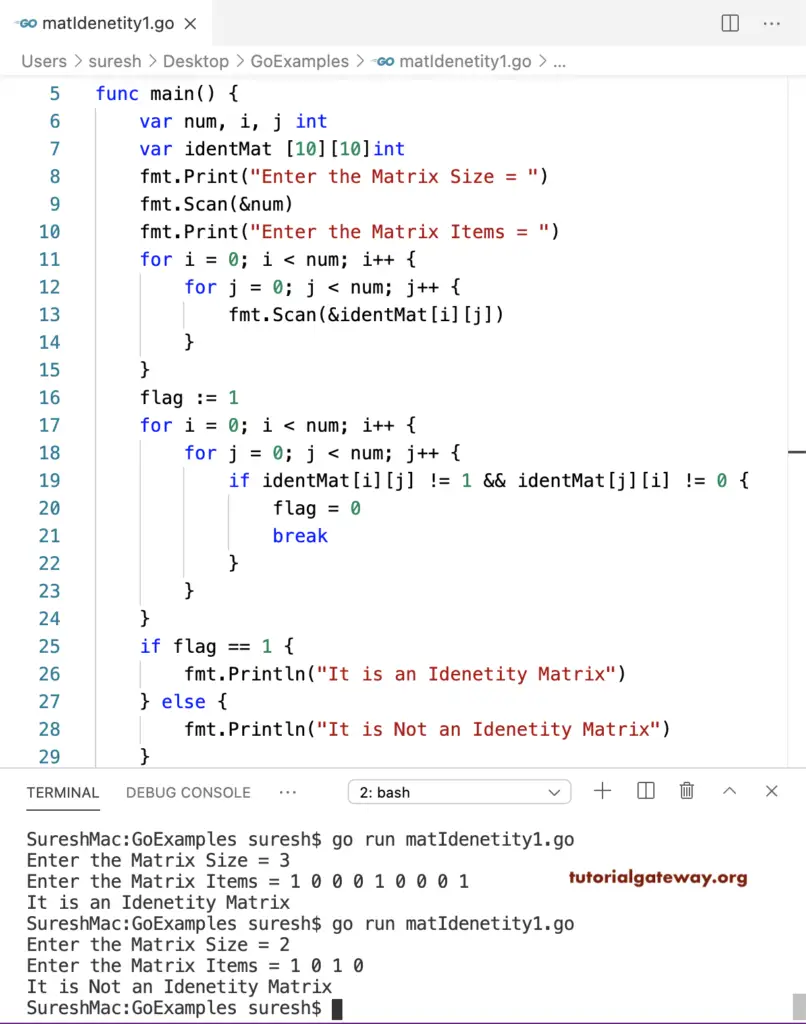
Write a Go program to check whether the given matrix is an identity matrix or not. Any square matrix is an identity matrix if its main diagonal items are ones and all the other values are zeros. Within the nested for loop, we used the if statement (if identMat[i][j] != 1 && identMat[j][i] != 0) to check whether the diagonals are not zeros and others are ones.

If any of the condition is true, assign zero to flag value, and the break statement will terminate the loop. The last If else statement (if flag == 1) prints the result based o notes flag value. 

package main

import "fmt"

func main() {
    var num, i, j int

    var identMat [10][10]int

    fmt.Print("Enter the Matrix Size = ")
    fmt.Scan(&num)

    fmt.Print("Enter the Matrix Items = ")
    for i = 0; i < num; i++ {
        for j = 0; j < num; j++ {
            fmt.Scan(&identMat[i][j])
        }
    }
    flag := 1
    for i = 0; i < num; i++ {
        for j = 0; j < num; j++ {
            if identMat[i][j] != 1 && identMat[j][i] != 0 {
                flag = 0
                break
            }
        }
    }
    if flag == 1 {
        fmt.Println("It is an Idenetity Matrix")
    } else {
        fmt.Println("It is Not an Idenetity Matrix")
    }
}

Golang Program to Check the Matrix is an Identity Matrix

In this Golang example, we used Else If to find the identity Matrix.

package main

import "fmt"

func main() {
    var rows, columns, i, j int

    var identMat [10][10]int

    fmt.Print("Enter the Matrix Rows and Columns = ")
    fmt.Scan(&rows, &columns)

    fmt.Print("Enter the Matrix Items = ")
    for i = 0; i < rows; i++ {
        for j = 0; j < columns; j++ {
            fmt.Scan(&identMat[i][j])
        }
    }
    flag := 1
    for i = 0; i < rows; i++ {
        for j = 0; j < columns; j++ {
            if (i == j) && (identMat[i][j] != 1) {
                flag = 0
            } else if (i != j) && (identMat[i][j] != 0) {
                flag = 0
            }
        }
    }
    if flag == 1 {
        fmt.Println("It is an Idenetity Matrix")
    } else {
        fmt.Println("It is Not an Idenetity Matrix")
    }
}

SureshMac:GoExamples suresh$ go run matIdentity2.go
Enter the Matrix Rows and Columns = 2 2
Enter the Matrix Items =  
1 0
0 1
It is an Idenetity Matrix
SureshMac:GoExamples suresh$ go run matIdentity2.go
Enter the Matrix Rows and Columns = 3 3
Enter the Matrix Items = 
1 0 0
0 0 1
0 1 0
It is Not an Idenetity Matrix