C Program to find Roots of a Quadratic Equation

How to write a C Program to find the Roots of a Quadratic Equation with an example? A Quadratic Equation in C can have two roots, and they depend entirely upon the discriminant. The mathematical representation of a Quadratic Equation is ax²+bx+c = 0. If discriminant > 0, then Two Distinct Real Roots will exist for this equation

If discriminant = 0, then Two Equal and Real Roots will exist, and the formula is shown below.

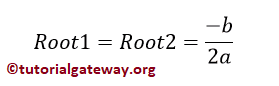
And if discriminant < 0, then Two Distinct Complex Roots will exist.

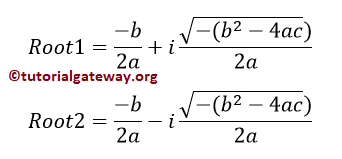
C Program to find Roots of a Quadratic Equation Using Else If

This program allows the user to enter three values for a, b, and c. Next, this c program finds the roots of a quadratic equation using the Else If Statement and sqrt function.

#include <stdio.h>
#include<math.h>
int main()
{
	float a, b, c;
	float root1, root2, imaginary, discriminant;
	
	printf("\n Please Enter values of a, b, c :  ");
  	scanf("%f%f%f", &a, &b, &c);
  	
  	discriminant = (b * b) - (4 * a *c);
  	
  	if(discriminant > 0)
  	{
  		root1 = (-b + sqrt(discriminant) / (2 * a));
  		root2 = (-b - sqrt(discriminant) / (2 * a));
		printf("\n Two Distinct Real Roots Exists: root1 = %.2f and root2 = %.2f", root1, root2);
  	}
  	else if(discriminant == 0)
  	{
  		root1 = root2 = -b / (2 * a);
  		printf("\n Two Equal and Real Roots Exists: root1 = %.2f and root2 = %.2f", root1, root2);
  	}
  	else if(discriminant < 0)
  	{
  		root1 = root2 = -b / (2 * a);
  		imaginary = sqrt(-discriminant) / (2 * a);
  		printf("\n Two Distinct Complex Roots Exists: root1 = %.2f+%.2f and root2 = %.2f-%.2f", root1, imaginary, root2, imaginary);
  	}
	
  	return 0;
}

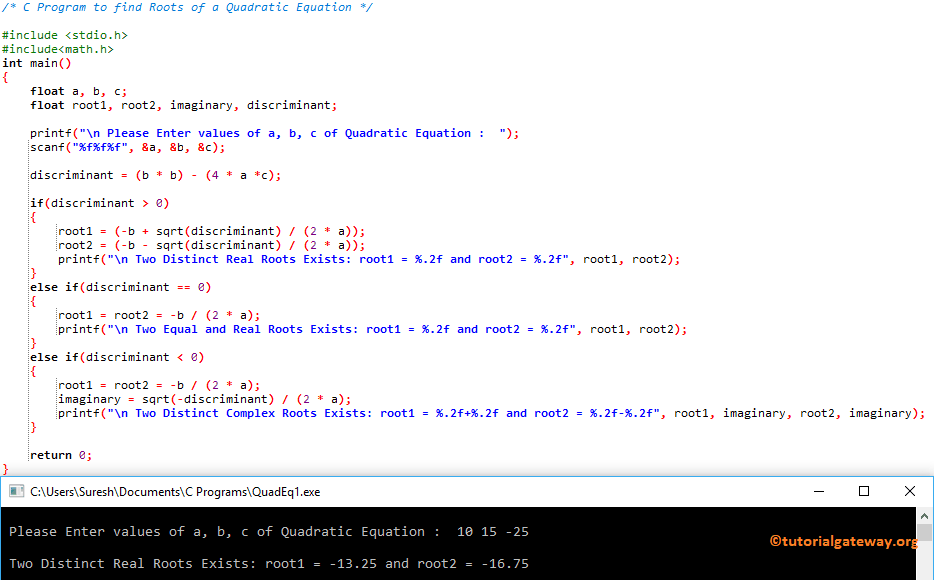
Within this C Program to find Roots of a Quadratic Equation example, the User entered Values 10, 15, and -25. It means a = 10, b = 15, c = -25 and the Quadratic equation is 10x²+15x-25 = 0

discriminant = (b * b) – (4 * a *c) = (15 * 15) – (4 * 10 *(-25))
discriminant = (225) – (- 1000) = 225 + 1000 = 1225

It means discriminant > 0, so
root1 = (-b + sqrt(discriminant) / (2 * a)) = (-15 + sqrt(1225) / (2 * 10))
root1 = (-15 + 35 / (20)) = -15 + 1.75 = -13.25

root2 = (-b – sqrt(discriminant) / (2 * a)) = (-15 – sqrt(1225) / (2 * 10))
root2 = (-15 – 35 / (20)) = -15 – 1.75 = -16.75

C Program to Calculate Roots of a Quadratic Equation Using Switch Case

This C program to find the roots of a quadratic equation is the same as above, but this time, we are using the Switch case in Programming.

#include <stdio.h>
#include<math.h>
int main()
{
	float a, b, c;
	float root1, root2, imaginary, discriminant;
	
	printf("\n Please Enter values of a, b, c :  ");
  	scanf("%f%f%f", &a, &b, &c);
  	
  	discriminant = (b * b) - (4 * a *c);
  	
  	switch(discriminant > 0)
  	{
  		case 1:
  			root1 = (-b + sqrt(discriminant) / (2 * a));
  			root2 = (-b - sqrt(discriminant) / (2 * a));
			printf("\n Two Distinct Real Roots Exists: root1 = %.2f and root2 = %.2f", root1, root2);
			break;
		case 0:
			switch(discriminant < 0)
			{
				case 1: //True
					root1 = root2 = -b / (2 * a);
					imaginary = sqrt(-discriminant) / (2 * a);
					printf("\n Two Distinct Complex Roots Exists: root1 = %.2f+%.2f and root2 = %.2f-%.2f", root1, imaginary, root2, imaginary);
					break;
				case 0: // False (Discriminant = 0)
					root1 = root2 = -b / (2 * a);
					printf("\n Two Equal and Real Roots Exists: root1 = %.2f and root2 = %.2f", root1, root2);
					break;
			}
  	}
	
  	return 0;
}

Within this C Program to find Roots example, User entered Values are 2 3 5. It means a = 2, b = 3, c = 5 and the Quadratic equation is 2x²+3x+5 = 0

discriminant = (b * b) – (4 * a *c) = (3 * 3) – (4 * 2 * 5)
discriminant = (9) – (40) = -31

It means discriminant < 0, so
root1 = root2 = -b / (2 * a)
root1 = root2 = -3 / (2 * 2) = -0.75

imaginary= sqrt(-discriminant) / (2 * a)
imaginary= sqrt(- -31) / (2 * 2) =  5.567 / 4 = 1.3919

root1= root1+imaginary
root1= -0.75+1.3919

root2= root2-imaginary
root2= -0.75-1.3919