How to write a C Program to find Upper Triangle Matrix with example?. An Upper triangle Matrix is a square matrix where elements below the main diagonal are zeros.
C Program to find Upper Triangle Matrix Example
This C program to find Upper Triangle Matrix allows the user to enter the number of rows and columns of a Matrix. Next, we are going to find the upper triangle matrix using For Loop.
#include<stdio.h>
int main()
{
int i, j, rows, columns, a[10][10];
printf("\n Please Enter Number of rows and columns : ");
scanf("%d %d", &i, &j);
printf("\n Please Enter the Matrix Elements \n");
for(rows = 0; rows < i; rows++)
{
for(columns = 0;columns < j;columns++)
{
scanf("%d", &a[rows][columns]);
}
}
for(rows = 0; rows < i; rows++)
{
printf("\n");
for(columns = 0; columns < j; columns++)
{
if(columns >= rows)
{
printf("%d ", a[rows][columns]);
}
else
{
printf("0 ");
}
}
}
return 0;
}
In this C Program to find Upper Triangle Matrix, We declared single Two dimensional arrays Multiplication of size of 10 * 10. The below statements asks the User to enter the Matrix size (Number of rows and columns. For instance 2 Rows, 2 Columns = a[2][2] )
printf("\n Please Enter Number of rows and columns : ");
scanf("%d %d", &i, &j);
Next, we used C Programming for loop to iterate each cell present in a[2][2] matrix. Conditions inside the C for loops ((rows < i) and (columns < j)) will ensure the compiler, not to exceed the 2D array in C limit. Otherwise, the matrix will overflow
scanf statement inside the for loop will store the user entered values in every individual array element such as a[0][0], a[0][1], …..
for(rows = 0; rows < i; rows++).
{
for(columns = 0; columns < j; columns++)
{
scanf("%d", &a[rows][columns]);
}
}
In the next program line, We have one more for loop to find the Upper Triangle of a Matrix
for(rows = 0; rows < i; rows++)
{
printf("\n");
for(columns = 0; columns < j; columns++)
{
if(columns >= rows)
{
printf("%d ", a[rows][columns]);
}
else
{
printf("0 ");
}
}
}
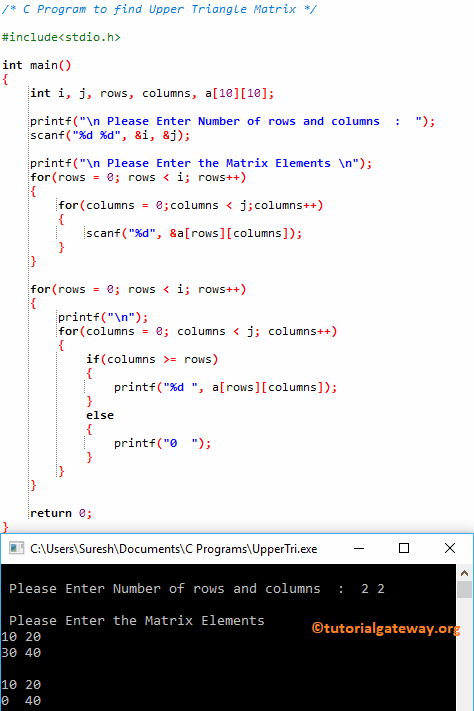
User inserted values for Upper Triangular Matrix are: a[2][2] = {{10, 20}, { 30, 40}}
The For Loop iteration behind this C Program to find Upper Triangle Matrix is:
Row First Iteration: for(rows = 0; rows < 2; 0++)
The condition (0 < 2) is True.
Column First Iteration: for(columns = 0; 0 < 2; 0++)
The condition (columns < 2) is True. So, it will start executing the statements inside the C program loop.
if(columns >= rows) => if(0 >= 0) – condition is True. So, it will print a[0][0] = 10
Column Second Iteration: for(columns = 1; 1 < 2; 1++)
The condition (columns < 2) is True.
if(columns >= rows) => if(1 >= 0) – condition is True. So, it will print a[0][1] = 20
Column Third Iteration: for(columns = 2; 2 < 2; 2++)
The condition (columns < 2) is False. So it will exit from the loop.
Next, rows value will increment to 1.
Row Second Iteration: for(rows = 1; rows < 2; 1++)
The condition (1 < 2) is True.
Column First Iteration: for(columns = 0; 0 < 2; 0++)
The condition (columns < 2) is True. So, it will start executing the statements inside the loop
if(columns >= rows) => if(0 >= 1) – This condition is False. So, it will print 0
Column Second Iteration: for(columns = 1; 1 < 2; 1++)
The condition (columns < 2) is True.
if(columns >= rows) => if(1 >= 1) – This condition is True. So, it will print a[1][1] = 40
Column Third Iteration: for(columns = 2; 2 < 2; 2++)
The condition (columns < 2) is False. So it will exit from the loop.
Next, rows value will increment to 1. After the increment, the condition inside the first for loop (rows < 2) will fail. So it will exit from the loop.
Let me try the same with the 3 * 3 matrix, and the Upper Triangle Matrix is. Refer to the Multi-Dimensional Array in C article.
Please Enter Number of rows and columns : 3 3
Please Enter the Matrix Elements
10 20 30
40 50 60
70 80 90
10 20 30
0 50 60
0 0 90 Also Read