Python Program to find Factorial of a Number

Factorial is denoted by the exclamation mark (!). We can define it as the product of all positive integers less than or equal to that number & greater than 0. For example, the factorial of 4 (4!) means 4 x 3 x 2 x 1, which equals 24. This blog post will explore how to write a Python program to find or calculate the factorial of a number efficiently.

We begin with a basic understanding of the factorial algorithm and how to calculate it in mathematics. Next, we show you different approaches to writing Python programs to find the factorial of a number using For Loop, While Loop, Functions, and Recursion.

The math or mathematical module in this programming language has a factorial() function that directly calculates and returns the results for any positive number. You can use this function by importing the math library.

Python Program to find the factorial of a Number using math function

The Mathematical Representation of the Factorial of n is represented as n!. Where n! = n * (n-1) * (n -2) * …….* 1. For instance, consider n = 5.

• 5! = 5 * (5 – 1) * (5 – 2) * (5 – 3) * (5 – 1)
• 5! = 5 x 4 x 3 x 2 x 1 = 120

It is denoted with the exclamation mark (!), and in this program code, we use the built-in math module factorial function on the number to find it.

import math 

a = int(input(" Please enter any Integer : "))

ft = math.factorial(a)
print("The Result of %d  = %d" %(a, ft))

In this example, we use the math prod() function that accepts the iteration value, finds the product of each value, and returns the factorial of a number.

import math

num = int(input("Enter any Number : "))

if num < 0:
    print("Please Enter Positive Integer Only.")
elif num == 0:
    print("The Fact of 0 = 1.")
else:
    fact = math.prod(range(1, num + 1))
    print(f"The Fact of {num} is {fact}.")

Python Program to find the Factorial of a Number using For Loop

This code allows the user to enter any integer. Using this given value, this program finds the Factorial of a number using For Loop. The for loop will start from 1 and multiply the current value by the next integer until it reaches the user given number.

number = int(input(" Please enter any Number : "))
fact = 1

for i in range(1, number + 1):
    fact = fact * i
print("The factorial of %d  = %d" %(number, fact))

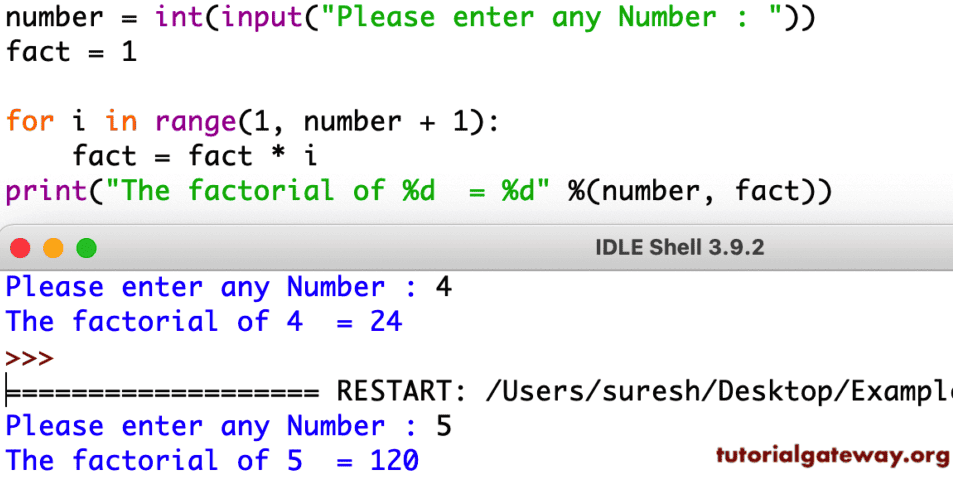
The user entered integer in the above program example is 4. Please refer to math functions, For Loop, While Loop, and Functions articles in Python.

First Iteration
i = 1, Fact = 1 and number = 5

Fact = Fact * i;
Fact = 1 * 1 = 1

2nd Iteration: i = 2, Fact = 1 and Number = 5
Fact = 1 * 2 = 2

3rd Iteration: i = 3, Fact = 2 and Number = 5
Fact = 2 * 3 = 6

4th Iteration: i = 4, Fact = 6 and Number = 5
Fact = 6 * 4 = 24

Next, i become 5. So, For loop Terminated.

The For Loop Time Complexity is O(n), and Space Complexity is O(1)

The above code for the factorial program returns 1 for the negative values. So, we need the If else statement to print a message for negative input.

num = int(input("Enter any Number : "))
fact = 1

if num < 0:
    print("Please Enter Positive Integer Only.")
else:
    for i in range(1, num + 1):
        fact = fact * i
    print("The factorial of %d  = %d" %(num, fact))

Enter any Number : -9
Please Enter Positive Integer Only.

Enter any Number : 6
The factorial of 6  = 720

Python Program to find the Factorial of a Number using while Loop

In this program, we just replaced the for loop with the while Loop to find the factorial of a number.

value = int(input(" Please enter any Value : "))
fact = 1
i = 1

while(i <= value):
    fact = fact * i
    i = i + 1

print("The Result of %d  = %d" %(value, fact))

Python Program to find the Factorial of a Number using Functions

This code is the same as the first example. However, we separated the factorial logic using the Functions.

def calculating(num):
    faco = 1

    for i in range(1, num + 1):
        faco = faco * i

    return faco


val = int(input(" Please enter any Value : "))

faco = calculating(val)
print("The Result of %d  = %d" %(val, faco))

Python Program for Factorial of a Number using Recursion

This code passes the user entered value to the Function. Within this recursive function, this example program finds the factorial of a number using the recursive function or recursively.

Within the user-defined function of this program, the If Else Statement checks whether the integer is Equal to 0 or 1. If the condition is TRUE, then the function returns 1. If the condition is False, the function recursively returns Num * (Num -1).

def factFind(num):
    if num < 0:
        print("Please Enter Positive Integer Only.")
    elif num == 0:
        return 1
    else:
        return num * factFind(num - 1)

num = int(input("Enter any Num : "))
print(f"Fact of {num} is {factFind(num)}.")

User Entered Value = 6.

Fac = num * factFind (num -1);
= 6 * factFind (5)
= 6 * 5 * factFind (4)
= 6 * 5 * 4 * factFind (3)
= 6 * 5 * 4 * 3 * factFind (2)
= 6 * 5 * 4 * 3 * 2 * factFind(1)
= 6 * 5 * 4 * 3 * 2
= 720

The Recursive function Time and Space Complexity are O(n).

Factorial using List comprehension

This Program finds the Factorial of a Number using list comprehension.

num = int(input("Enter any Number : "))

if num < 0:
    print("Please Enter Positive Integer Only.")
elif num == 0:
    print("The Fact of 0 = 1.")
else:
    fact = 1
    [fact := fact * i for i in range(1, num + 1)]
    print(f"The Fact of {num} is {fact}.")

Enter any Number : 5
The Fact of 5 is 120.

Factorial using the lambda reduce function

This Python Program for the Factorial of a Number example uses the lambda and reduce functions.

from functools import reduce

num = int(input("Enter any Number : "))

if num < 0:
    print("Please Enter Positive Integer Only.")
elif num == 0:
    print("The Fact of 0 = 1.")
else:
    fact = reduce(lambda a, b: a * b, range(1, num + 1), 1)
    print(f"The Fact of {num} is {fact}.")

This example is the same as the above. However, it uses the lambda recursive function.

from functools import reduce

def factorial(num):
    return reduce(lambda a, b: a * b, range(1, num + 1), 1)

num = int(input("Enter any Number : "))

if num < 0:
    print("Please Enter Positive Integer Only.")
elif num == 0:
    print("The Fact of 0 = 1.")
else:
    print(f"The Fact of {num} is {factorial(num)}.")

Enter any Number : 0
The Fact of 0 = 1.