Java Ternary Operator 3

Java Ternary Operator

The Java Ternary Operator also called a Conditional Operator. The Java Ternary or Conditional operator mostly used in the decision making process to return true or false. This ternary operator returns the statement depends upon the given expression result. The basic syntax of a Conditional Operator in Java Programming is as shown below:

Test_expression ? statement1: statement2

If the given test condition or boolean expression evaluates to true, then Java conditional operator will return statement1. If the condition evaluates to false, then statement2 is returned.

Java Ternary Operator example

In this Program, we are going to use the Ternary or Conditional Operator to find whether the person is eligible to vote or not.

package JavaOperators;

import java.util.Scanner;

public class TernaryOperator {
	private static Scanner sc;

	public static void main(String[] args) {
		int age;
		sc = new Scanner(System.in);
		System.out.println(" Please Enter Your Age: ");
		age = sc.nextInt();
		
		String Message = (age >= 18)? " You are eligible to Vote " : 
					      " You are Not eligible to Vote ";
		System.out.println(Message);
		
		/** REPLACE THE ABOVE CODE WITH FOLLOWING CODE
		 * 		System.out.println((age >= 18)? 
		 *		" You are eligible to Vote":
                 *       "You are Not eligible to Vote");
		 */			
	}
}

This Java Ternary Operator program allows the user to enter his or her age and assign the user entered integer value to the age variable. If the user entered value is 18 or above, then it will assign the first statement after the ? symbol to String variable Message. ” You are eligible to Vote “

If he/she enters below 18, then the second statement (which is after the : symbol) will be assigned to String variable Message. ” You are Not eligible to Vote “

Finally, we are using the Java System.out.println statement to print the string data inside the Message variable

 Please Enter Your Age: 
15
 You are Not eligible to Vote

Let us try with a different value

 Please Enter Your Age: 
29
 You are eligible to Vote

Nested Conditional Operator in Java example

In this Program, we are going to use the Nested Ternary Operator in Java to find whether the person is eligible to work or not.

  1. In this java ternary operator example, We declared a string variable called Message, and we assigned this variable to the conditional functionality.
  2. The first condition checks whether age is less than 18. If this condition is True, then it will return the first value after the ? symbol, which is You are too Young to Work
  3. When the first condition in the Ternary fails, then it will execute the variable after : symbol. By using Nested conditional operator we are checking one more condition here (age >= 18 && age <= 60). If this condition is True, then it will return the first value after the ? symbol, which is You are eligible to Work
  4. If the Nested condition of a conditional fails, then ternary operator java will execute the variable after : symbol, which is You are too Old to Work.
package JavaOperators;

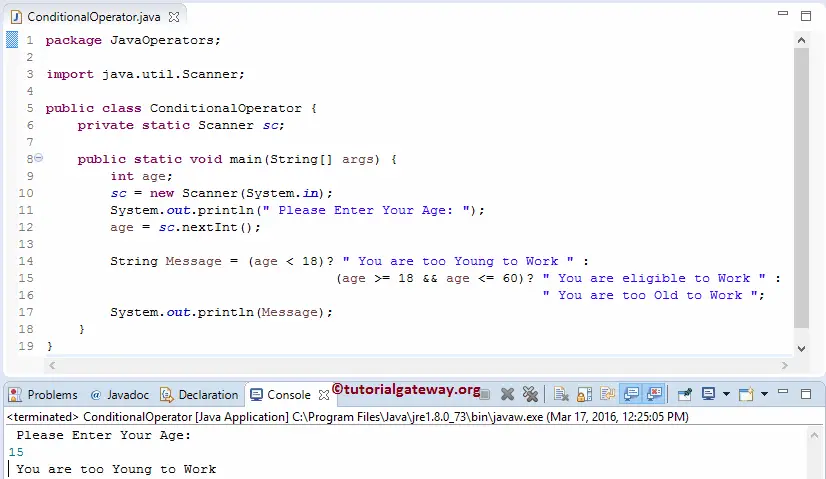
import java.util.Scanner;

public class ConditionalOperator {
	private static Scanner sc;

	public static void main(String[] args) {
		int age;
		sc = new Scanner(System.in);
		System.out.println(" Please Enter Your Age: ");
		age = sc.nextInt();

		String Message = (age < 18)? " You are too Young to Work " :
                    		  	     (age >= 18 && age <= 60)? " You are eligible to Work ": 
                    				      		       " You are too Old to Work ";
		System.out.println(Message);
	}
}
Java Ternary Operator 3

Output 2

 Please Enter Your Age: 
28
 You are eligible to Work
 Please Enter Your Age: 
65
 You are too Old to Work