C Program to find Determinant of a Matrix

How to write a C Program to find Determinant of a Matrix with example. Below image will show you the mathematical formula behind this program

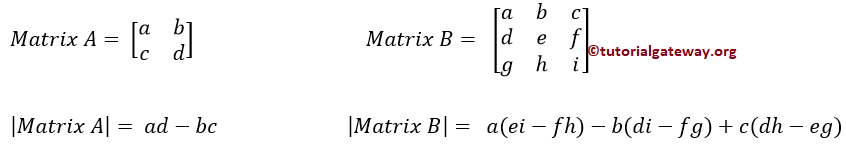
C Program to find Determinant of a Matrix – 2 * 2 Example

This program allows the user to enter the rows and columns elements of a 2 * 2 Matrix. Next, we are going to find the determinant of this matrix.

/* C Program to find Determinant of a Matrix  - 2 * 2 */
 
#include<stdio.h>
 
int main()
{
 	int rows, columns, a[2][2], Deter = 0;
  
 	printf("\n Please Enter the 2 * 2 Matrix Elements \n ");
 	for(rows = 0; rows < 2; rows++)
  	{
   		for(columns = 0;columns < 2; columns++)
    	{
      		scanf("%d", &a[rows][columns]);
    	}
  	}
     
	Deter = (a[0][0] * a[1][1]) - (a[0][1] * a[1][0]);
  	
  	printf("\n The Determinant of 2 * 2 Matrix = %d", Deter);
 	return 0;
}

 Please Enter the 2 * 2 Matrix Elements 
 10 20
30 40

 The Determinant of 2 * 2 Matrix = -200

In this program, we used for loop to iterate each cell present in a[2][2] matrix. Conditions inside the for loops((rows < i) and (columns < j)) will ensure the compiler, not to exceed the Matrix limit. Otherwise, the matrix will overflow

The C Programming scanf statement inside the for loop will store the user entered values in every individual array element such as a[0][0], a[0][1], …..

for(rows = 0; rows < i; rows++).
{
  for(columns = 0; columns < j; columns++)
   {
     scanf("%d", &a[rows][columns]);
   }
}

In the next line, We are calculating the Determinant

Determinant = (a[0][0] * a[1][1]) - (a[0][1] * a[1][0]);

User entered array a[2][2] = {{10, 20}, {30, 40}}

Determinant = (a[0][0] * a[1][1]) – (a[0][1] * a[1][0])

Determinant= (10 * 40) – (20 * 30)

Determinant= (400) – (600) = -200

C Program to find Determinant of a Matrix – 3 * 3 Example

This program is similar to the above example, but this time we are finding the determinant of 3 * 3 matrix.

/* C Program to find Determinant of a Matrix  - 3 * 3 */
 
#include<stdio.h>
 
int main()
{
 	int rows, columns, a[3][3];
	int x, y, z, Determinant = 0;
  
 	printf("\n Please Enter the 3 * 3 Matrix Elements \n");
 	for(rows = 0; rows < 3; rows++)
  	{
   		for(columns = 0;columns < 3; columns++)
    	{
      		scanf("%d", &a[rows][columns]);
    	}
  	}
  	
    x = (a[1][1] * a[2][2]) - (a[2][1] * a[1][2]);
    y = (a[1][0] * a[2][2]) - (a[2][0] * a[1][2]);
    z = (a[1][0] * a[2][1]) - (a[2][0] * a[1][1]);
	
	Determinant = (a[0][0] * x) - (a[0][1] * y) + (a[0][2] * z);
  	
  	printf("\n The Determinant of 3 * 3 Matrix = %d", Determinant);
 	return 0;
}

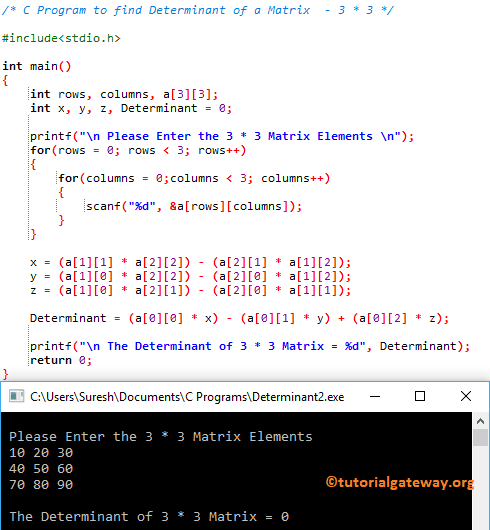
In this C Program to find Determinant of a Matrix example, User entered array a[3][3] = {{10, 20, 30}, {40, 50, 60}, {70, 80, 90}}

x = (a[1][1] * a[2][2]) – (a[2][1] * a[1][2])

x = (50 * 90) – (80 * 60)

x = 4500 – 4800

x = -300

y = (a[1][0] * a[2][2]) – (a[2][0] * a[1][2])

y = (40 * 90) – (70 * 60)

y = 3600 – 4200

y = -600

z = (a[1][0] * a[2][1]) – (a[2][0] * a[1][1])

z = (40 * 80) – (70 * 50)

z = (3200) – (3500)

z = -300

Determinant= (a[0][0] * x) – (a[0][1] * y) + (a[0][2] * z)

Determinant = (10 * -300) – (20 * -600) + (30 * -300)

= (-3000) – (-12000) + (-9000)

Determinant= -3000 + 12000 – 9000 = 0